[선형대수] 4.3 Cholesky Decomposition ~ 4.4 Eigendecomposition and Diagonalization

공부하는 단계에서 정리한 내용입니다.

잘못된 내용이 있다면 말씀해주시면 감사하겠습니다.

https://mml-book.github.io/book/mml-book.pdf

 

4.3 Cholesky Decomposition

행렬도 분해할 수 있다.

여러 가지 방법이 있는데 우리는 Cholesky decomposition/ Cholesky factorization에 대해서 알아볼 것이다.

(숫자에서의 제곱근처럼 행렬을 분해하는 방법이라서 symmetric, positive definite 한 행렬에만 적용할 수 있음)

 

 

Theorem 4.18 (Cholesky Decomposition)

Symmetric하고 positive definite한 행렬 $A$는 $A = LL^{\top}$으로 분해할 수 있다.

여기서 $L$을 $A$의 Cholesky factor라고 부르고, diagonal element들을 포함한 unique한 lower trianglular matrix이다.

 

 

 

Ex 4.10 (Cholesky Factorization)

아래와 같은 방법으로 $a$를 가지고 $l$을 구할 수 있다.

 

이러한 Cholesky decomposition은 아래와 같은 상황들에서 유용하게 쓰인다.

- 머신러닝에서 수치계산을 할 때

   e.g. covariance matrix, multivariate Gaussian variable

- 깊은 확률 모델(e.g. VAE)의 기울기를 계산할 때

    확률변수를 linear transformation 시킴

- Determinant를 계산할 때

    $det(A) = det(L)det(L^T) = {det(L)}^2$이고, L이 삼각행렬이기 때문에 $det(A)$는 대각 원소들의 곱의 제곱이 된다.

 

 

 

4.4 Eigendecomposition and Diagonalization

 

Diagonal matrix는 대각 원소들을 제외한 나머지 원소들이 0인 행렬이다.

이때 determinant는 대각 원소들의 곱이 되고, power는 대각 원소를 제곱이 된다. 역행렬은 각각의 대각 원소에 역수만 취하면 된다.

 

그래서 이번 section에서는 행렬을 diagonal 형태로 바꾸는 방법에 대해서 알아볼 것이다. 

행렬 $A$가 diagonal matrix $D$와 유사한 경우($D = P^{-1}AP$) 중에서도 특별한 경우($D$가 $A$의 eigenvalue를 diagonal element로 가지는 행렬)를 살펴볼 것이다.

 

 

Def 4.19 (Diagonalizable)

Diagonal matirx $D$에 대해서, 만약 $D = P^{-1}AP$인 $P$가 존재하면 $A$가 diagonalizable 하다고 한다.

 

(이 부분 잘 와닿지가 않는다.. 이걸 왜 하는거지)

$A$를 diagonalizing 하는 것은 선형 변환을 다른 basis로 표현하는 것과 같다. 그리고 이러한 basis는 $A$의 eigenvector들이다.

왜 새로운 basis들이 $A$의 eigenvector들이 되는지 과정을 전개하면서 알아볼 것이다.

 $n \times n$ 행렬 $A$가 있고, 스칼라 $\lambda_1, ..., \lambda_n$와 벡터 $p_1, ..., p_n$이 있다고 하자.

 

$P = \begin{bmatrix} p_1, ..., p_n \end{bmatrix}$이고 $D = \begin{bmatrix} \lambda_1 & 0 & 0 & \cdots & 0 \\ 0 & \lambda_2 & 0 & \cdots & 0 \\ 0 & 0 & \lambda_3 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & \lambda_n  \end{bmatrix}$ 일 때,

$AP = PD$ 이면 $\lambda$들이 $A$의 eigenvalue고 $P$가 $A$의 eigenvector 이다.

증명은 아래와 같다.

 

 

 

Theorem 4.20 (Eigendecomposition)

$n \times n$ 행렬 $A$의 eigenvector들이 서로 linearly independent해서 basis를 이룰 때,  $A$는 diagonalizable 하다.

행렬 $D$는 diagonal matrix이고, 그 대각 원소들은 $A$의 eigenvalue 들이다.

 

 

 

Theorem 4.21

Symmetric한 행렬은 항상 diagonalized 될 수 있다.

 

 

 

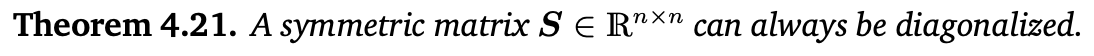
Remark.

Defective한 행렬의 decomposition을 할 때 Jordan normal form을 사용할 수 있지만, 이 책에서는 다루지 않는다.

 

 

 

Geometric Intuition for the Eigendecomposition

(직관적으로 이해하라고 했지만 직관적으로 이해가 안 됨)

일단 이해한 내용만 적어보겠다. 다음과 같은 순서대로 진행된다.

$P^{-1}$이 basis를 standard basis에서 eigenbasis로 바꾼다.

그리고 diagonal $D$가 $p_1, p_2$를 eigenbasis 축을 따라서 $\lambda_i$만큼 스케일링 한다.

이렇게 스케일링 된 벡터들을 $P$가 다시 standard/canonical coordinate로 변환한다.

수식으로 표현하면 아래와 같아서 결론적으로 $A = PDP^{-1}$이다.

 

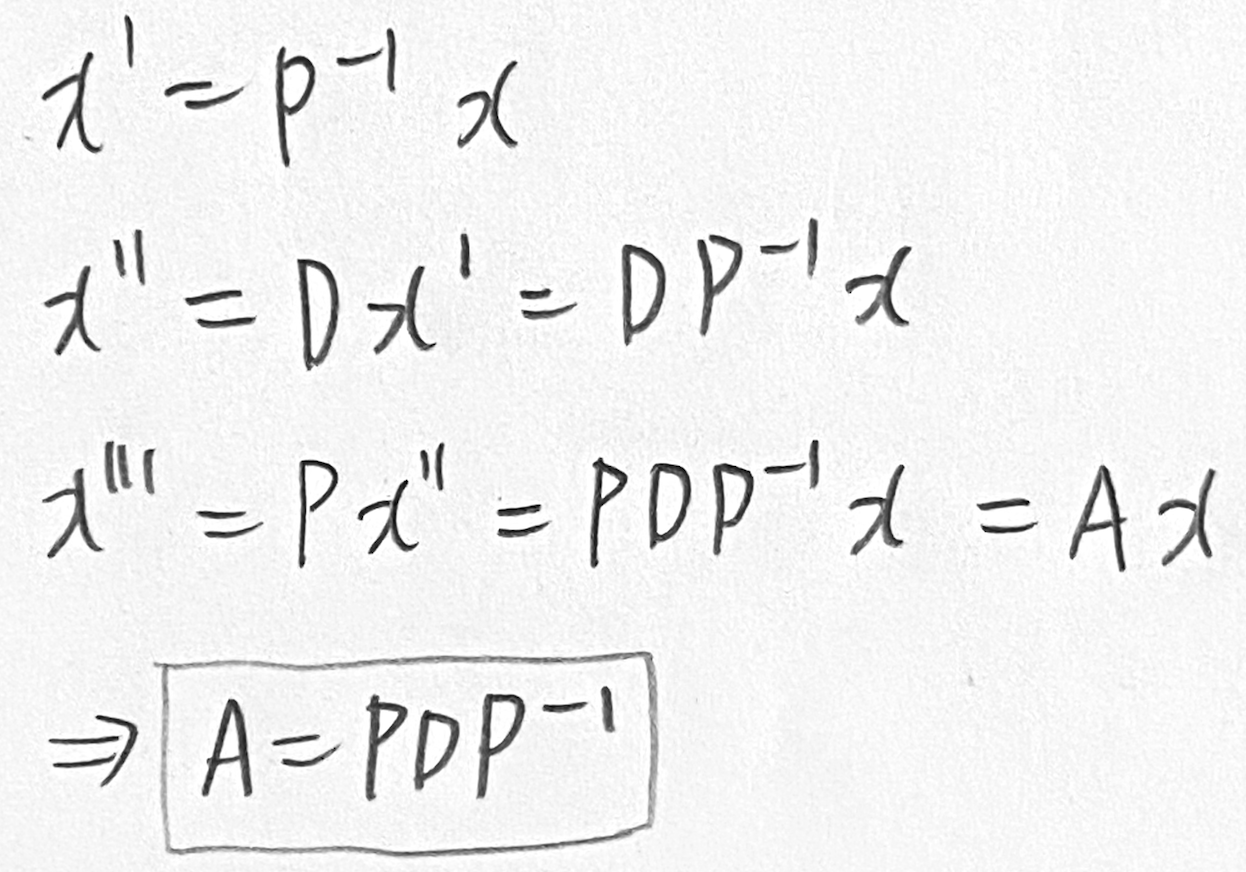
과정 자체는 이해했지만 이걸 왜 하는지 잘 모르겠다. 일단 나중을 위해 교재 사진은 첨부한다.

 

 

 

Ex 4.11 (Eigendecomposition)

$A = \frac{1}{2} \begin{bmatrix} 5 & -2 \\ -2 & 5 \end{bmatrix}$의 eigendecomposition을 구해보자.

아래와 같이 3단계를 거치면 된다.

 

이러한 성질을 활용해서 아래의 계산들을 쉽게 할 수 있다.

  - $A^k = (PDP^{-1})^k = PDP^{-1} \times PDP^{-1} \times \cdots \times PDP^{-1} = P D^{k} P^{-1}$ 이다.

  - $A = PDP^{-1}$이 존재할 때, 

      $det(A) = det(PDP^{-1}) = det(P)det(D)det(P^{-1})$

                                                    $=det(D)$  $(\because det(P^{-1}) = \frac{1}{det(P)})$

                                                    $= \prod_{i} d_{ii}$

 

 

 

지금까지 $n \times n$ 행렬에만 eigenvalue decomposition을 했다.

이제 $m \times n$ 행렬에 decomposition을 하는 singular value decomposition에 대해서 배워볼 것이다.