공부하는 단계에서 정리한 내용입니다.
잘못된 내용이 있다면 말씀해주시면 감사하겠습니다.
https://mml-book.github.io/book/mml-book.pdf
4.2 Eigenvalues and Eigenvectors
이제 행렬과 그 linear mapping을 eigen이라는 개념을 통해서 새롭게 표현해볼 것이다.
Def 4.6
$n \times n$ 행렬 $A$에 대해서 $\lambda$를 eigenvalue라고 하고, $A$가 $Ax = \lambda x$를 만족할 때 $x$를 $A$의 eigenvector라고 한다. 그리고 이 식을 eigenvalue equation 이라고 부른다.
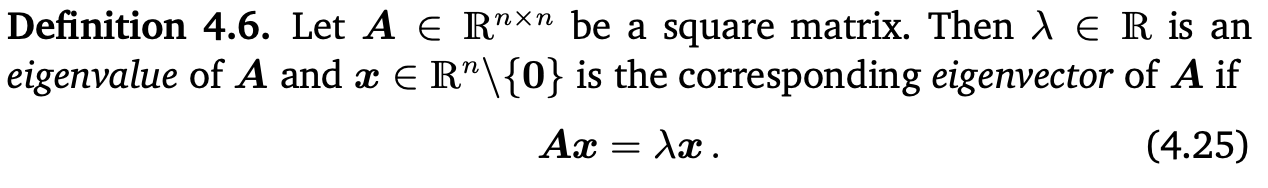
Remark
관습적으로 eigenvalue를 내림차순으로 정렬한 뒤 순서대로 first, second, .. eigenvalue/eigenvector 라고 부르기도 한다.
하지만 책에 따라 다르게 정의되는 경우가 많기 때문에, 이 책에서는 eigenvalue들이 특성 순서대로 정렬되어 있다고 간주하지 않는다.
아래 표현들은 모두 같은 표현들이다.
• $\lambda$가 $n \times n$ 행렬 $A$의 eigenvalue이다.
• $Ax = \lambda x$를 만족하는 $x \neq 0$인 벡터가 존재한다. (와닿지가 않는다.. 일단 패스)
• $rk(A - \lambda I_n) < n$
$A - \lambda I$의 rank가 n이면 모든 행과 열이 독립적이고, $(A - \lambda I)x=0$의 유일한 해는 $x=0$이 된다.
하지만 rank가 n보다 작다면 $x \neq 0$인 해가 존재할 수 있다. (이거랑 위에거랑 연결되는 것 같은데..)
• $det(A - \lambda I_n) = 0$
$\lambda$가 존재하려면 역행렬이 존재하지 않아야 하고 역행렬이 존재하지 않는 조건은 $det$값이 0이 될 때이다.
Def 4.7 (Collinearity and Codirection)
두 벡터가 같은 방향을 가리킬 때 codirected라고 하고, 그냥 같은 직선에 있을 때는 collinear라고 한다.

Remark (Non-uniqueness of eigenvectors)
아래와 같은 식을 통해 만약 $x$가 eigenvector라면, 0이 아닌 상수 $c$를 곱한 $cx$도 eigenvector임을 알 수 있다.
$$A(cx) = c(Ax) = c(\lambda x) = \lambda (cx)$$
벡터 $x$에 collinear한 모든 벡터는 $A$의 eigenvector라는 것이다.
즉, eigenvector의 크기는 중요하지 않고 방향만 중요하다!
Theorem 4.8
행렬 $A$의 eigenvalue $\lambda$는 해당 행렬의 characteristic polynomial인 $p_{A}(\lambda)$의 해와 같다.

글로만 들으니 와닿지가 않아서 예시를 하나 들어봤다.

결론적으로 $A = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}$일 때 eigenvalue는 $\lambda = 1,3$이고, 각각의 eigenvector는 $x = \begin{bmatrix} 1 \\ -1 \end{bmatrix}, \begin{bmatrix} 1 \\ 1 \end{bmatrix}$이다.
Def 4.9
Algebraic multiplicity는 각각의 $\lambda_{i}$가 몇번 중복되는지 나타내는 숫자이다.

이것도 예시를 하나 들어봤다. 역시 예시를 들으니 이해가 잘 된다.

Def 4.10 (Eigenspace and Eigenspectrum)
모든 eigenvector들의 집합이 이루는 부분공간을 eigenspace라고 한다. 기호로는 $E_{\lambda}$와 같이 쓴다.
그리고 모든 eigenvalue들의 집합을 eigenspectrum 혹은 그냥 spectrum이라고 한다.

즉 eigenspace $E_\lambda$는 $(A - \lambda I)x = 0$의 해집합이다.
기하학적으로 봤을 때, eigenvector는 늘어나는 방향을 의미하고 eigenvalue는 늘어나는 정도를 의미한다.
만약 eigenvalue가 음수이면 반대 방향으로 늘어난다는 것이다.
Ex 4.4 (The Case of the Identity Matrix)
행렬 $A$가 $I$일 때, $p_{I}(\lambda) = det(I - \lambda I) = (1 - \lambda)^n = 0$이 되므로 eigenvalue가 $\lambda = 1$ 하나밖에 없다.
따라서 유일한 eigenspace $E_1$은 $n$차원이고,
$n$차원의 모든 standard basis($e_1 = \begin{bmatrix} 1 \\ 0 \\ 0 \\ . \\ . \\ 0 \end{bmatrix}, e_2 = \begin{bmatrix} 0 \\ 1 \\ 0 \\ . \\ . \\ 0 \end{bmatrix}, e_n = \begin{bmatrix} 0 \\ 0 \\ 0 \\ . \\ . \\ 1 \end{bmatrix}$)들은 $I$의 eigenvector가 된다.
(마지막 부분 조금 이해 안 가지만 일단 그렇구나 하기로 했음)
Eigenvalue와 eigenvector의 중요한 성질들은 다음과 같다.
• 행렬 $A$와 $A^{\top}$은 같은 eigenvalue를 가지지만 다른 eigenvector를 가진다.
• Eigenspace $E_\lambda$는 $A - \lambda I$의 null space와 같다.
Null space 자체가 행렬을 곱했을 때 0이 되는 벡터들의 집합을 나타내기 때문이다.
• Similar matrix들은 같은 eigenvalue를 가진다. 따라서 eigenvalue도 basis change에 불변하는 값이다.
• Symmetric하고 positive definite한 행렬은 항상 양의 실수 eigenvalue를 가진다.
Ex 4.5 (Computing Eigenvalues, Eigenvectors, and Eigenspaces)
$A = \begin{bmatrix} 4 & 2 \\ 1 & 3 \end{bmatrix}$의 eigenvalue와 eigenvector를 구하는 방법을 알아보자. (앞에서 혼자 조금 해보길 잘했다)
아래와 같은 3단계를 거쳐야 한다.
Step1: Characteristic Polynomial
Step2: Eigenvalues
Step3: Eigenvectors and Eigenspaces
책에 나온 예시 그대로 전개하면서 eigenvalue와 eigenspace들을 구해봤다. 그냥 단계 따라가면서 구하면 구해진다.

Def 4.11
하나의 eigenvalue $\lambda_i$에 대한 독립적인 eigenvector의 개수를 $\lambda_{i}$의 geometric multiplicity라고 한다.
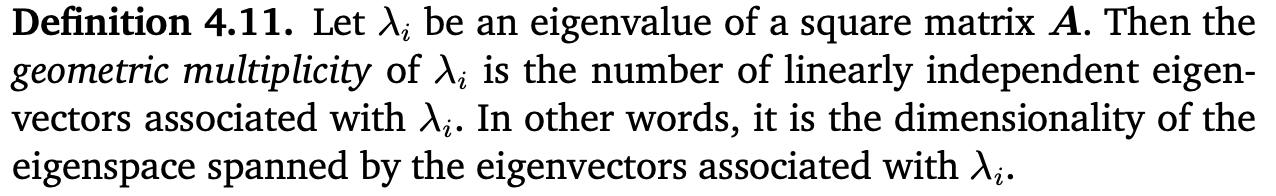
즉, span의 개수를 세면 된다. 위 예시에서는 $E_{\lambda_1}$과 $E_{\lambda_2}$ 모두 geometric multiplicity가 1이다.
Remark. Algebraic multiplicity와 Geometric multiplicity의 관계
Algebraic multiplicity는 Geometric multiplicity보다 크거나 같다.
즉, $gm(\lambda) \leq am(\lambda)$ 이다.
위의 예시로 보면 더 와닿는다.
$A = \begin{bmatrix} 2 & 1 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{bmatrix}$ 일 때, $det(A - \lambda I) = (2 - \lambda)^2 (3 - \lambda)$이므로 $\lambda_1 = 2$이고 $\lambda_2 = 3$이다.
각각의 algebraic multiplicity는 2,1 이다.
각각의 geometric multiplicity는 1,1이다. ($\because E_2 = span \left\{\begin{bmatrix} -1 \\ 1 \\ 0 \end{bmatrix} \right\}$, $E_3 = span \left\{\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \right\}$)
Ex 4.6 Algebraic multiplicity와 Geometric multiplicity
행렬 $A$의 algebraic multiplicity와 geometric multiplicity를 각각 구하면 아래와 같다.
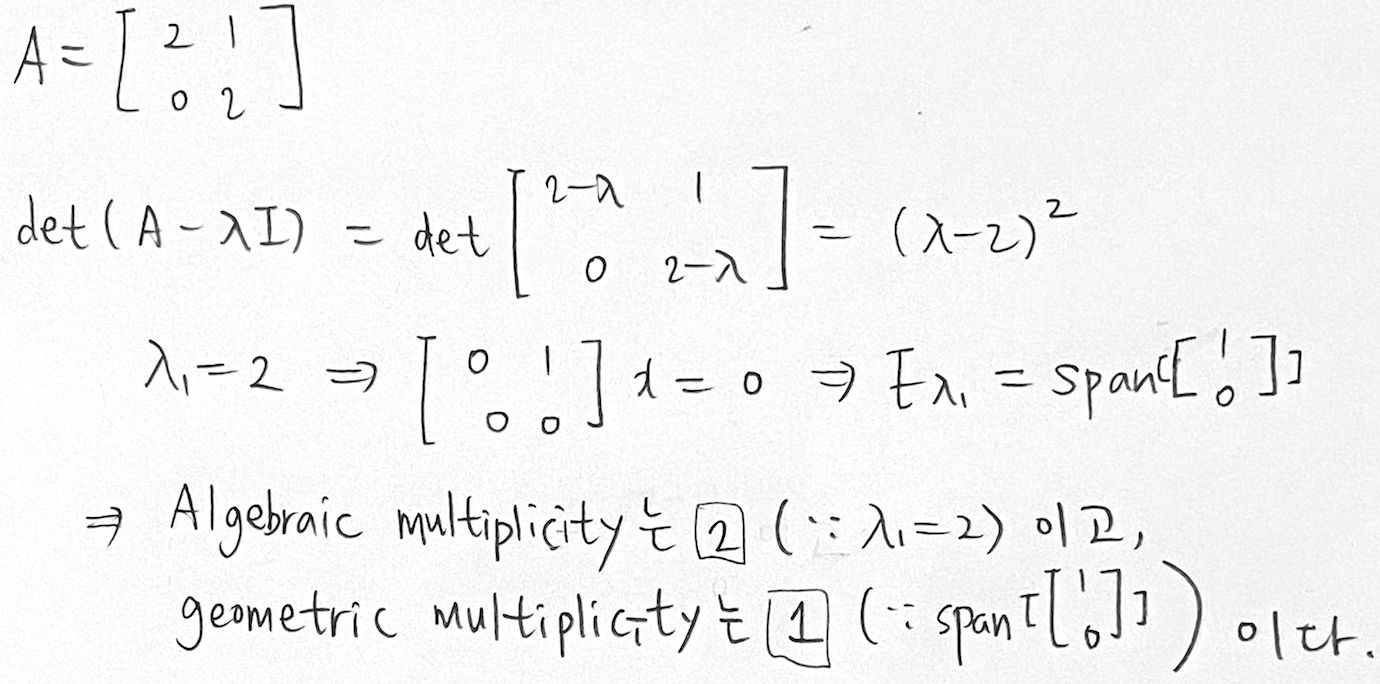
챕터 하나가 매우 길다.. 이어서 다음 글에서 graphical intuition in two dimensions에 대해서 공부해볼 것이다.
'선형대수' 카테고리의 다른 글
| [선형대수] 4.3 Cholesky Decomposition ~ 4.4 Eigendecomposition and Diagonalization (1) | 2025.03.13 |
|---|---|
| [선형대수] 4.2 Eigenvalues and Eigenvectors(Graphical Intuition in Two Dimensions~) (0) | 2025.03.11 |
| [선형대수] 4.1 Determinant and Trace (Determinant's properties ~) (0) | 2025.03.09 |
| [선형대수] 4.1 Determinant and Trace (~Ex 4.3 Laplace Expansion) (0) | 2025.03.08 |
| [선형대수] 4. Matrix Decompositions (0) | 2025.03.07 |
