공부하는 단계에서 정리한 내용입니다.
잘못된 내용이 있다면 말씀해주시면 감사하겠습니다.
https://mml-book.github.io/book/mml-book.pdf

4.2 Eigenvalues and Eigenvectors
이제 행렬과 그 linear mapping을 eigen이라는 개념을 통해서 새롭게 표현해볼 것이다.
Def 4.6
n×n 행렬 A에 대해서 λ를 eigenvalue라고 하고, A가 Ax=λx를 만족할 때 x를 A의 eigenvector라고 한다. 그리고 이 식을 eigenvalue equation 이라고 부른다.

Remark
관습적으로 eigenvalue를 내림차순으로 정렬한 뒤 순서대로 first, second, .. eigenvalue/eigenvector 라고 부르기도 한다.
하지만 책에 따라 다르게 정의되는 경우가 많기 때문에, 이 책에서는 eigenvalue들이 특성 순서대로 정렬되어 있다고 간주하지 않는다.
아래 표현들은 모두 같은 표현들이다.
• λ가 n×n 행렬 A의 eigenvalue이다.
• Ax=λx를 만족하는 x≠0인 벡터가 존재한다. (와닿지가 않는다.. 일단 패스)
• rk(A−λIn)<n
A−λI의 rank가 n이면 모든 행과 열이 독립적이고, (A−λI)x=0의 유일한 해는 x=0이 된다.
하지만 rank가 n보다 작다면 x≠0인 해가 존재할 수 있다. (이거랑 위에거랑 연결되는 것 같은데..)
• det(A−λIn)=0
λ가 존재하려면 역행렬이 존재하지 않아야 하고 역행렬이 존재하지 않는 조건은 det값이 0이 될 때이다.
Def 4.7 (Collinearity and Codirection)
두 벡터가 같은 방향을 가리킬 때 codirected라고 하고, 그냥 같은 직선에 있을 때는 collinear라고 한다.

Remark (Non-uniqueness of eigenvectors)
아래와 같은 식을 통해 만약 x가 eigenvector라면, 0이 아닌 상수 c를 곱한 cx도 eigenvector임을 알 수 있다.
A(cx)=c(Ax)=c(λx)=λ(cx)
벡터 x에 collinear한 모든 벡터는 A의 eigenvector라는 것이다.
즉, eigenvector의 크기는 중요하지 않고 방향만 중요하다!
Theorem 4.8
행렬 A의 eigenvalue λ는 해당 행렬의 characteristic polynomial인 pA(λ)의 해와 같다.

글로만 들으니 와닿지가 않아서 예시를 하나 들어봤다.

결론적으로 A=[2112]일 때 eigenvalue는 λ=1,3이고, 각각의 eigenvector는 x=[1−1],[11]이다.
Def 4.9
Algebraic multiplicity는 각각의 λi가 몇번 중복되는지 나타내는 숫자이다.

이것도 예시를 하나 들어봤다. 역시 예시를 들으니 이해가 잘 된다.

Def 4.10 (Eigenspace and Eigenspectrum)
모든 eigenvector들의 집합이 이루는 부분공간을 eigenspace라고 한다. 기호로는 Eλ와 같이 쓴다.
그리고 모든 eigenvalue들의 집합을 eigenspectrum 혹은 그냥 spectrum이라고 한다.

즉 eigenspace Eλ는 (A−λI)x=0의 해집합이다.
기하학적으로 봤을 때, eigenvector는 늘어나는 방향을 의미하고 eigenvalue는 늘어나는 정도를 의미한다.
만약 eigenvalue가 음수이면 반대 방향으로 늘어난다는 것이다.
Ex 4.4 (The Case of the Identity Matrix)
행렬 A가 I일 때, pI(λ)=det(I−λI)=(1−λ)n=0이 되므로 eigenvalue가 λ=1 하나밖에 없다.
따라서 유일한 eigenspace E1은 n차원이고,
n차원의 모든 standard basis(e1=[100..0],e2=[010..0],en=[000..1])들은 I의 eigenvector가 된다.
(마지막 부분 조금 이해 안 가지만 일단 그렇구나 하기로 했음)
Eigenvalue와 eigenvector의 중요한 성질들은 다음과 같다.
• 행렬 A와 A⊤은 같은 eigenvalue를 가지지만 다른 eigenvector를 가진다.
• Eigenspace Eλ는 A−λI의 null space와 같다.
Null space 자체가 행렬을 곱했을 때 0이 되는 벡터들의 집합을 나타내기 때문이다.
• Similar matrix들은 같은 eigenvalue를 가진다. 따라서 eigenvalue도 basis change에 불변하는 값이다.
• Symmetric하고 positive definite한 행렬은 항상 양의 실수 eigenvalue를 가진다.
Ex 4.5 (Computing Eigenvalues, Eigenvectors, and Eigenspaces)
A=[4213]의 eigenvalue와 eigenvector를 구하는 방법을 알아보자. (앞에서 혼자 조금 해보길 잘했다)
아래와 같은 3단계를 거쳐야 한다.
Step1: Characteristic Polynomial
Step2: Eigenvalues
Step3: Eigenvectors and Eigenspaces
책에 나온 예시 그대로 전개하면서 eigenvalue와 eigenspace들을 구해봤다. 그냥 단계 따라가면서 구하면 구해진다.

Def 4.11
하나의 eigenvalue λi에 대한 독립적인 eigenvector의 개수를 λi의 geometric multiplicity라고 한다.
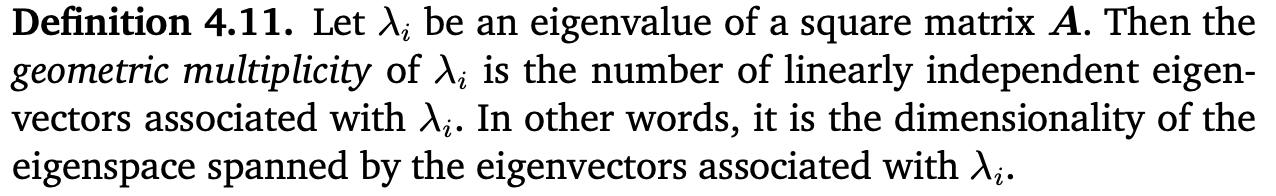
즉, span의 개수를 세면 된다. 위 예시에서는 Eλ1과 Eλ2 모두 geometric multiplicity가 1이다.
Remark. Algebraic multiplicity와 Geometric multiplicity의 관계
Algebraic multiplicity는 Geometric multiplicity보다 크거나 같다.
즉, gm(λ)≤am(λ) 이다.
위의 예시로 보면 더 와닿는다.
A=[210020003] 일 때, det(A−λI)=(2−λ)2(3−λ)이므로 λ1=2이고 λ2=3이다.
각각의 algebraic multiplicity는 2,1 이다.
각각의 geometric multiplicity는 1,1이다. (∵, E_3 = span \left\{\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \right\})
Ex 4.6 Algebraic multiplicity와 Geometric multiplicity
행렬 A의 algebraic multiplicity와 geometric multiplicity를 각각 구하면 아래와 같다.
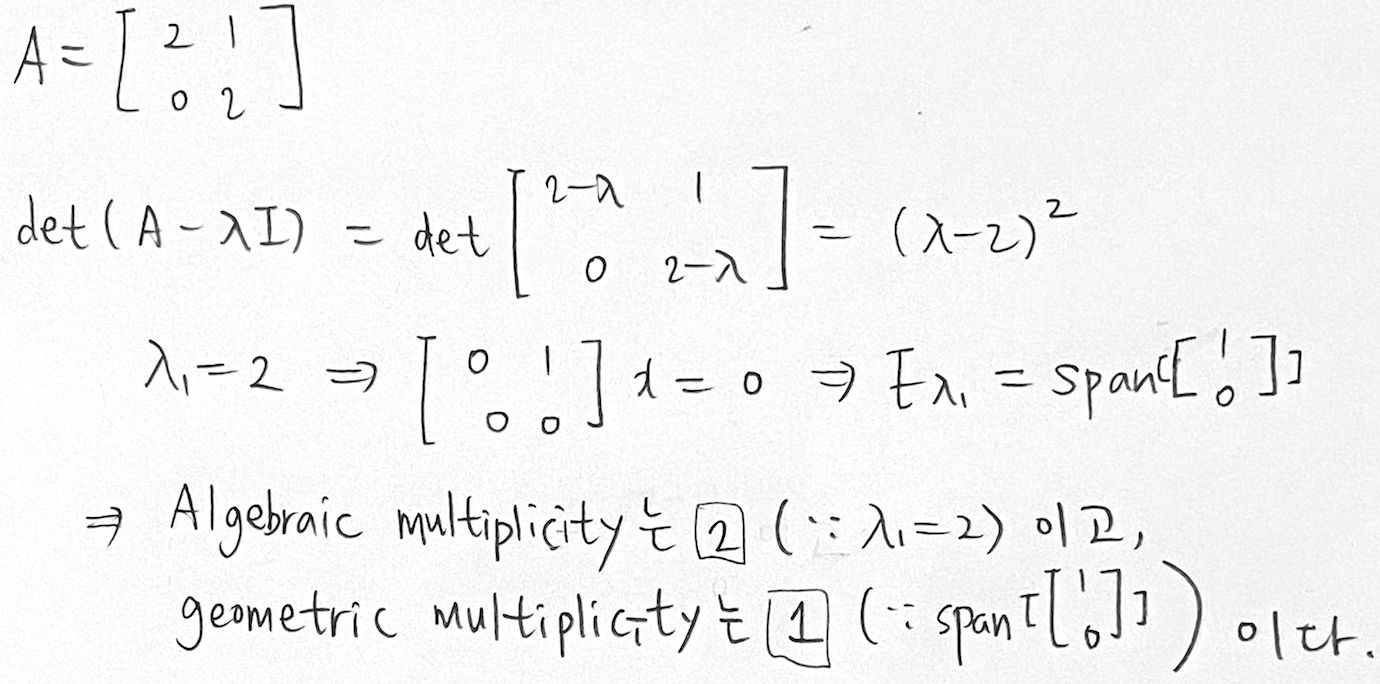
챕터 하나가 매우 길다.. 이어서 다음 글에서 graphical intuition in two dimensions에 대해서 공부해볼 것이다.
'선형대수' 카테고리의 다른 글
| [선형대수] 4.3 Cholesky Decomposition ~ 4.4 Eigendecomposition and Diagonalization (1) | 2025.03.13 |
|---|---|
| [선형대수] 4.2 Eigenvalues and Eigenvectors(Graphical Intuition in Two Dimensions~) (0) | 2025.03.11 |
| [선형대수] 4.1 Determinant and Trace (Determinant's properties ~) (0) | 2025.03.09 |
| [선형대수] 4.1 Determinant and Trace (~Ex 4.3 Laplace Expansion) (0) | 2025.03.08 |
| [선형대수] 4. Matrix Decompositions (0) | 2025.03.07 |