공부하는 단계에서 정리한 내용입니다.
잘못된 내용이 있다면 말씀해주시면 감사하겠습니다.
https://mml-book.github.io/book/mml-book.pdf
4.5 Singular Value Decomposition
선형대수에서 SVD(singular value decomposition)는 중요한 matrix decomposition 방법이다.
모든 행렬에 적용할 수 있고, 항상 존재하기 때문이다.
그리고 SVD를 통해서 선형변환 $\phi: V \rightarrow W$이 벡터 공간의 구조를 어떻게 바꾸는지 기하학적으로 설명할 수 있다.
Theorem 4.22 (SVD Theorem)
$m \times n$ 행렬 $A$가 있을 때, $A$의 SVD 공식은 아래와 같다.
$$A = U \Sigma V^{\top}$$

대각 행렬 $\Sigma$의 diagonal element들을 singular values 라고 한다. Singular value들은 보통 내림차순으로 정렬되어 있다.
$U$ 행렬의 열벡터들을 left singular vectors 라고 한다.
$V$ 행렬의 열벡터들을 right singular vectors 라고 한다.
$m \times n$ 행렬 $\Sigma$는 유일하고, 아래와 같이 $m$과 $n$의 크기에 따라서 모양이 달라진다.

$m \leq n$ 일 때는 diagonal 구조 밑에 0벡터들이 채워지고, $m \geq n$ 일 때는 diagonal 구조 옆에 0벡터들이 채워진다.
Remark.
모든 $m \times n$ 행렬 $A$에 대해서 SVD를 구할 수 있다.
4.5.1 Geometric Intuitions for the SVD
변환 행렬 $A$의 변환과정을 SVD를 통해서 직관적으로 이해해보자.
이전 section에서 eigendecomposition을 직관적으로 이해했을 때와 비슷한 방식으로 SVD를 이해해볼 수 있다.
대략적으로 말하면, SVD에서 $V^{\top}$은 첫 번째 basis change를, $\Sigma$는 스케일링과 증강을, 그리고 $U$는 두 번째 basis change를 담당한다.
이제 더 자세하게 살펴볼 것이다.
Linear transformation $\phi: \mathbb R^n \rightarrow \mathbb R^m$이 있다고 하자.
Standard basis가 $B, C$이고, $\mathbb R^n$의 또 다른 기저를 $\tilde{B}$, $\mathbb R^m$의 또 다른 기저를 $\tilde{C}$라고 하자.
그리고 아래 그림과 같은 과정을 거친다.
(★★★★★★★★★★★★★★★★★★★★★★★ 이 부분이 핵심 ★★★★★★★★★★★★★★★★★★★★★★★)

① 행렬 $V^{\top}$가 basis를 $B (= v_1, v_2)$ (기존 기저)에서 $\tilde{B} (=e_1, e_2)$ (새로운 기저)로 바꾼다.
기하학적으로 회전에 해당한다.
② $\Sigma$는 새로운 좌표계에서 좌표를 $\sigma_i$만큼 스케일링 하고, 차원을 추가하거나 제거한다.
$m > n$이면 차원이 증가하고, $m < n$이면 차원이 감소한다. 그리고 변환된 벡터들은 새로운 좌표계 $\tilde{C}$에 위치된다.
③ 행렬 $U$가 벡터 $\sigma_1 u_1, \sigma_2 u_2$를 basis $\tilde{C}$ (새로운 기저)에서 $C$ (표준 기저)로 바꾼다.
빨간색 벡터 $\sigma_1 u_1$와 주황색 벡터 $\sigma_2 u_2$는 $e_1-e_2$ 평면에서 회전해서 새로운 방향으로 정렬된다.
(★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★)
Eigendecomposition은 같은 공간 안에서 basis 변환이 이루어지고, 다시 원래 basis로 표현된다.
하지만 SVD는 서로 다른 공간 $\mathbb R^m$과 $\mathbb R^n$에서 모두 basis를 변환한다.
즉, SVD는 서로 다른 두 공간을 연결할 수 있다.
Ex 4.12 (Vectors and the SVD)
한 변의 길이가 2이고 원점을 중심으로 하는 정사각형이 변환 $A$에 의해서 어떻게 바뀌는지 알아보자.
$A = U \Sigma V^{\top}$ 은 아래에 계산되어 있다. (계산 방법은 다음 section에서 배우는 듯하다)

과정
① 행렬 $V^{\top}$으로 정사각형을 회전시킨다.
② Singular value 행렬 $\Sigma$를 적용해서 정사각형을 스케일링 한 뒤, 새로운 좌표계 $\mathbb R^3$으로 이동시킨다.
여전히 모든 벡터는 $x_1 - x_2$ 평면에 위치하고 있다.
③ 행렬 $U$로 정사각형을 $\mathbb R^3$에서 회전시킨다. 이제 벡터들이 $x_1 - x_2$ 평면에 있지 않다.
그림은 아래와 같다.
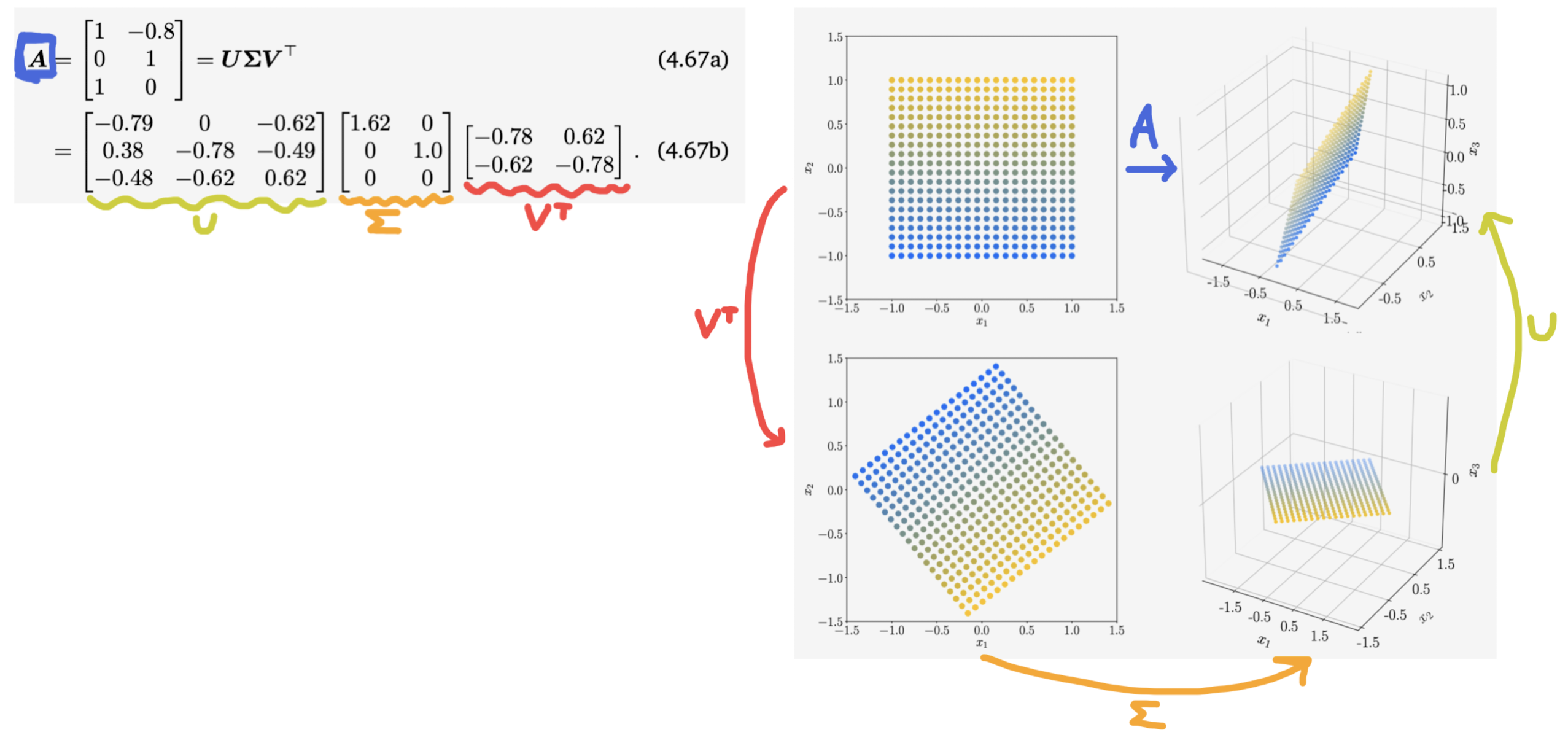
정리하자면, SVD는
행렬이 벡터를 변형하는 방식을 분해(회전 → 스케일링 → 다시 회전) 해서 알아보는 방법이다!
후.. 어렵다
공들여 이해하니 뿌듯하긴 하다
