[선형대수] 4.1 Determinant and Trace (~Ex 4.3 Laplace Expansion)

공부하는 단계에서 정리한 내용입니다.

잘못된 내용이 있다면 말씀해주시면 감사하겠습니다.

https://mml-book.github.io/book/mml-book.pdf

 

4.1 Determinant and Trace

앞에서 배웠듯이 행렬 $A \in \mathbb R^{n \times n}$의 determinant은 $A$를 $\mathbb R$로 대응시키는 함수이다.

쓸 때는 $det(A)$ 혹은 $\begin{vmatrix} A \end{vmatrix}$와 같이 쓴다.

 

 

 

Ex 4.1 (Testing for Matrix Invertibility)

행렬 $A \in R^{n \times n}$을 $n$의 크기에 따라서 살펴보자.

(i) $A$가 $1 \times 1$ 행렬 $a$일 때:

   $A$의 역행렬은 $A^{-1} = \frac{1}{a}, (a \neq 0)$가 된다.

(ii) $A$가 $2 \times 2$ 행렬일 때:

   $A A^{-1} = I$이므로, $A^{-1}$을 전개하면 아래와 같다.

$$A^{-1} = \frac{1}{a_{11} a_{22} - a_{12} a_{21}} \begin{bmatrix} a_{22} & -a_{12} \\ -a_{21} & a_{11} \end{bmatrix},    (a_{11} a_{22} - a_{12} a_{21} \neq 0)$$  

  여기서 $det(A) = \begin{vmatrix} a_{11} & -a_{12} \\ -a_{21} & a_{22} \end{vmatrix} = a_{11} a_{22} - a_{12} a_{21}$이다.

 

 

Ex 4.1을 살펴보면서 determinant와 역행렬의 존재여부의 관계에 대해서 어렴풋이 알 수 있었다.

아래의 Theorem 4.1은 이를 확장시켜서 행렬 $A$가 $n \times n$ 크기의 일 때 $det(A)$를 구하는 방법을 알려준다.

 

 

 

Theorem 4.1

모든 $n \times n$ 행렬 $A$에 대해서, $det(A) \neq 0$이면 $A$의 역행렬이 존재한다.

 

 

$n=1$일 때, $det(A) = det(a_{11}) = a_{11}$ 이고,

 

$n=2$일 때, $det(A) = \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} = a_{11}a_{22} - a{12}a_{21}$이고,

 

$n=3$일 때, $det(A) = \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix}$

 

                                   $= a_{11}a_{22}a_{33} + a_{21}a_{32}a_{13} + a_{31}a_{12}a_{23} - (a_{31}a_{22}a_{13} + a_{11}a_{32}a_{23} + a_{21}a_{12}a_{33})$이다.

 

(+ 팁: 왼쪽에서 오른쪽으로, 오른쪽에서 왼쪽으로 선을 그어가면서 기억하면 쉽다.)

 

그리고 triangular matrix들(Upper, lower triangular matrix)에서 $det(A)$는 대각선 원소들의 곱이다.

식으로 나타내면 아래와 같다.

$$det(T) = \prod_{i=1}^{n} T_{ii}$$

 

 

Ex 4.2 (Determinants as Measures of Volume)

Determinant를 단순한 수학 연산이 아니라 $n$개의 벡터가 만드는 공간적 구조를 실수 값으로 변환하는 함수로 해석할 수 있다.

이렇게 해석할 때, $det(A)$를 행렬 $A$의 열벡터들이  형성하는 $n$차원 평행육면체(parallelepiped)의 signed volume으로 볼 수 있다.

 

$n=2$일 때, 행렬 $A=\begin{bmatrix} b,g \end{bmatrix}$의 열벡터들은 $0, b, g, b+g$를 꼭짓점으로 하는 평행사변형(parallelogram)이 된다.

이때 $b,g$의 linearly independent 여부에 따라 $det(A)$값이 달라진다.

 

  (i) $b,g$가 linearly dependent

      $b,g$가 일직선에 있으므로 $det(A) = 0$이다.

 

  (ii) $b,g$가 linearly independent

      $b,g$를 $b = \begin{bmatrix} b \\ 0 \end{bmatrix}$와 $g = \begin{bmatrix} 0 \\ g \end{bmatrix}$로 쓸 수 있을 때,  $det(A) = \begin{vmatrix} b & 0 \\ 0 & g \end{vmatrix} = bg - 0 = bg$이다.

 

      이는 평행사변형 구하는 공식 (면적 = 높이 x 밑변)으로 이해될 수 있다.

 

여기서 나오는 determinant의 부호는 그냥 standard basis $e_1, e_2$와 비교했을 때의 상대적인 $b,g$의 방향을 나타낸다. 

양수면 반시계방향, 음수면 시계방향을 의미한다.

그리고 아래와 같이 벡터의 순서를 바꾸면 determinant의 부호만 바뀐다. 즉, 벡터의 순서를 바꾸면 평행사변형의 방향이 반대가 된다는 뜻이다.

 

이러한 직관을 고차원에도 적용할 수 있다. $\mathbb R^3$에서는 3개의 벡터가 평행육면체(parallelepiped)의 세 모서리를 구성하고, $det(A)$의 절댓값이 이 평행육면체의 부피를 의미한다.

 

$e.g.$ $r = \begin{bmatrix} 2 \\ 0 \\ -8 \end{bmatrix}$, $g = \begin{bmatrix} 6 \\ 1 \\ 0 \end{bmatrix}$, $b = \begin{bmatrix} 1 \\ 4 \\ -1 \end{bmatrix}$이고 $A = \begin{bmatrix} r, g, b \end{bmatrix}$일 때, 

 

        $V = | det(A) | = \begin{bmatrix} 2 & 6 & 1 \\ 0 & 1 & 4 \\ -8 & 0 & -1 \end{bmatrix} = 186$ 이다.

 

 

지금까지는 $3 \times 3$ 행렬의 determinant까지만 구했는데, 더 일반화해서 $n \times n$ 행렬의 determinant를 구하는 방법을 알아보려고 한다. 이때, Laplace expansion을 사용해서 $n \times n$ 행렬의 determinant를 구할 때 $(n-1) \times (n-1)$ 행렬의 determinant를 사용하고, 이를 재귀적으로 적용해서 결국 $2 \times 2$ 행렬의 determinant만 사용하도록 해서 계산을 줄일 수 있다.

 

 

 

Theorem 4.2 (Laplace Expansion)

$det(A)$를 구할 때 행 또는 열을 기준으로 아래와 같이 전개하면 된다고 한다.

 

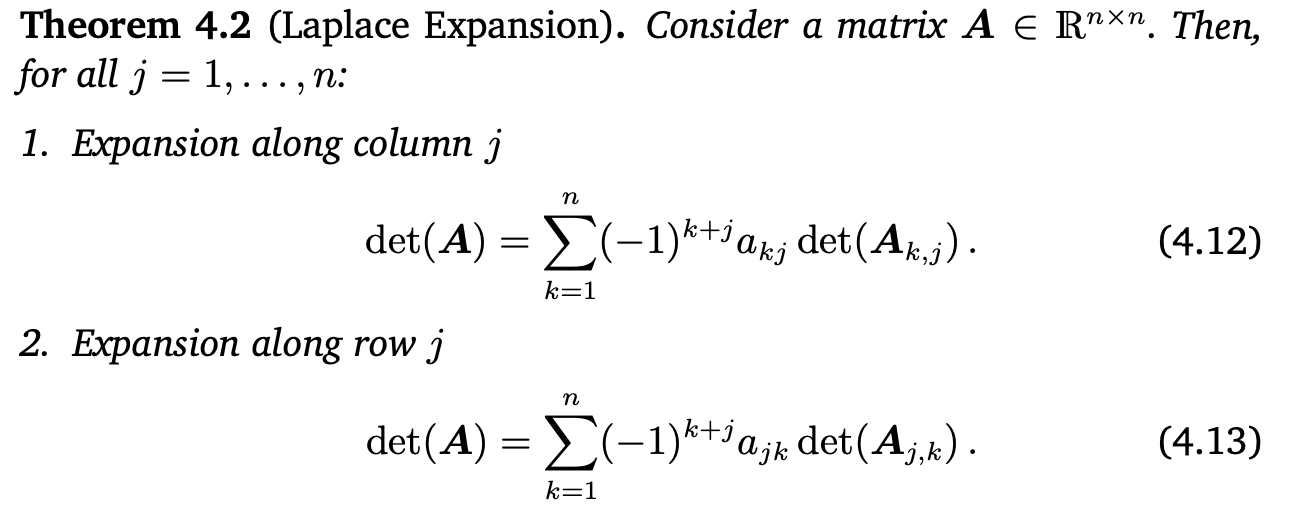
식으로 봤을 때 와닿지가 않기 때문에 아래 예시에서 직접 전개해보려고 한다.

 

 

 

Ex 4.3 (Laplace Expansion)

 

$A = \begin{bmatrix} 1 & 2& 3 \\ 3 & 1 & 2 \\ 0 & 0 & 1 \end{bmatrix}$의 determinant를 laplace expansion을 사용해서 구해보자. 추가로 검산은 Sarrus's Rule로 해볼 수 있다.

 

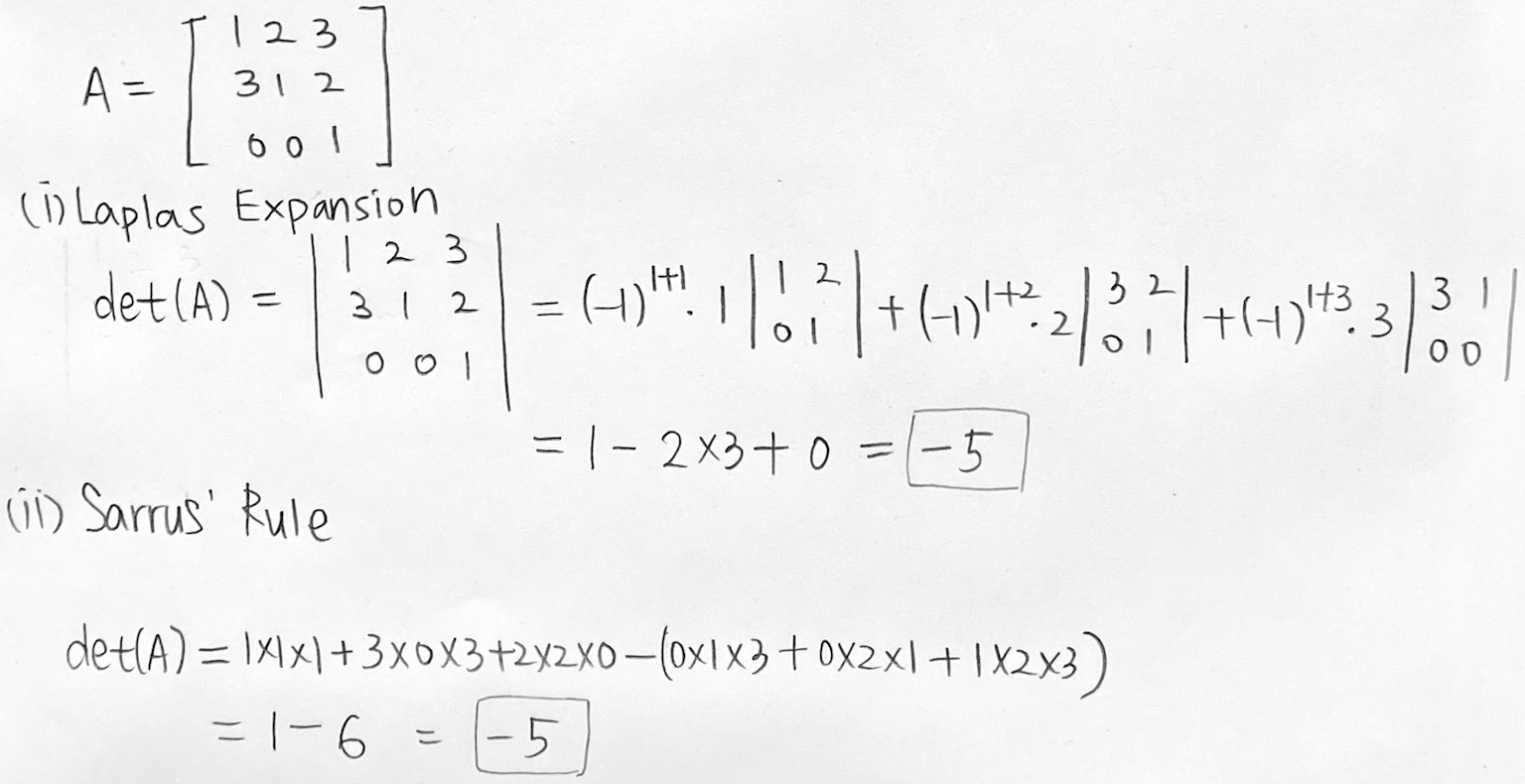
Laplas expansion과 Sarrus' Rule 모두 det(A) 값이 같게 나옴을 알 수 있다. 상황에 맞춰서 편한 걸 사용하면 될 듯하다.

 

다음에는 이어서 determinant의 성질들에 대해서 알아볼 것이다.