공부하는 단계에서 정리한 내용입니다.
잘못된 내용이 있다면 말씀해주시면 감사하겠습니다.
https://mml-book.github.io/book/mml-book.pdf
4.6 Matrix Approximation
지금까지 행렬 $A$를 $A = U \Sigma V^{\top}$으로 분해시키는 방법에 대해서 알아봤다.
이제 $A$ SVD로 전체 분해하는 방법 대신에, low-rank 행렬 $A_i$들의 합으로 나타내는 방법을 알아볼 것이다.
SVD를 전체 분해할 때보다 계산 비용이 적게 든다!
$m \times n$ 행렬 $A$는 아래와 같이 rank-1 행렬들의 합으로 나타낼 수 있다.
$$A = \sum_{i=1}^r \sigma_i u_i {v_i}^{\top}$$
$u_i$와 ${v_i}^{\top}$는 각각 SVD에서 등장하는 $U$와 $V$의 $i$번째 열벡터이다.
(+ 원래 $A = U \Sigma V^{\top}$꼴인데 왜 $\sigma_i$가 앞으로 빠졌냐면, $\sigma_i$가 스칼라 값이기 때문에 앞으로 빼도 상관 없기 때문이다!
$\Sigma$는 diagonal matrix이므로 $\begin{bmatrix} \sigma_1 & 0 & \cdots & 0 \\ 0 & \sigma_2 & \cdots & 0 \\ \ddots & \ddots & \vdots & \ddots \\ 0 & 0 & \cdots & \sigma_r \end{bmatrix}$ 꼴을 띈다. $\sigma_i$들은 각각의 $u_i {v_i}^{\top}$에 대응되는 축으로만 곱해진다.)
와닿지가 않아서 앞에서 사용한 행렬 $A = \begin{bmatrix} 1 & 0 & 1 \\ -2 & 1 & 0 \end{bmatrix}$을 가져와서 아래와 같이 rank-1 행렬들을 직접 계산해봤다.

아래 그림들은 스톤헨지의 흑백 이미지를 행렬로 변환한 다음 rank-1 행렬들로 분해한 것이다.

그림(a)는 $1,432 \times 1,910$ 크기의 원본 이미지이고, 그림(b)~그림(f)는 $A_1$~$A_5$ 사이의 rank-1 행렬이다.
그림(b)의 $A_1$ (여기서는 $u_1 {v_1}^{\top}$)에 가중치 $\sigma_1 \thickapprox 228,052$가 곱해지고, 그림(c)의 $A_2$ (여기서는 $u_2 {v_2}^{\top}$)에 가중치 $\sigma_2 \thickapprox 20,647$이 곱해지고, $A_3, A_4, A_5$도 이런식으로 곱해진 다음 모두 더해져서 원본이미지 (a)가 탄생한다.
여기서 만약에 $1$부터 $r$까지 다 더하지 않고 $1$부터 $k$까지만 더하고 싶다면($k < r$) 아래와 같이 쓰면 된다.
이를 rank-k approximation 이라고 한다. 말 그대로 $rk(\hat{A}(k)) = k$가 된다.
$$\hat{A}(k) := \sum_{i=1}^{k} \sigma_i u_i {v_i}^{\top}$$
아래 그림은 스톤헨지의 흑백이미지를 행렬로 변환한 다음 low-rank approximations $\hat{A}(k)$ 를 적용한 것이다.

$\hat{A}(5)$로 갈수록 바위들이 눈에 띄게 선명해짐을 알 수 있다.
Rank 행렬을 사용하면 기존 SVD를 사용할 때보다 계산량이 엄청나게 줄어든다.
SVD에서는 숫자가 총 $1,432 \times 1,910$개 필요하지만,
Rank 행렬을 사용하는 방법은 아래와 같이 숫자 $5(1 + 1,432 + 1,910)$개만 필요하다. (SVD의 0.6%만큼 정도만 있으면 된다!)

$\hat{A}(k)$와 기존 행렬 $A$와의 오차를 구하려면 norm 개념을 사용해야 한다.
Def 4.23 (Spectral Norm of a Matrix)
0이 아닌 모든 $n$차원 실수에 대해서 spectral norm은 다음과 같다.
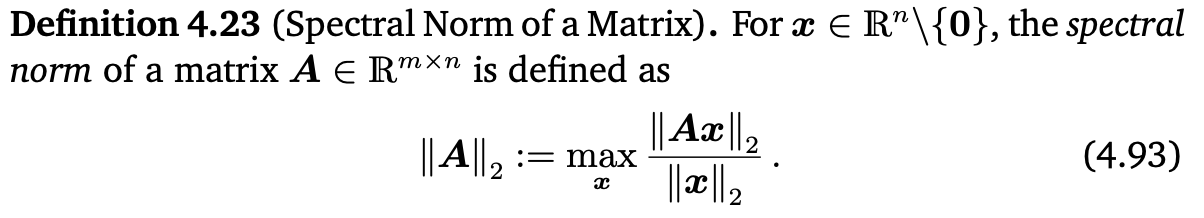
Spectral norm은 $x$에 행렬 $A$가 곱해졌을 때 얼마나 길어질 수 있는지를 나타낸다.
좌변의 $\| A \|_2$는 matrix norm이고, 우변의 $\| x \|_2$는 euclidean vector norm이다.
Theorem 4.24
행렬 $A$의 spectral norm $\| A \|_2$은 가장 큰 singular value $\sigma_1$ 값이다.
이에 대한 증명은 뒤에 exercise에서 해볼거임
Theorem 4.25 (Eckart-Young Theorem (Eckart and Young, 1936))
$m \times n$ 크기 행렬 $A$와 $B$가 있다고 하자. 각각의 rank는 $r, k( k \leqslant r)$이다.
Rank가 $k$인 행렬 $B$ 중에서 $A$와 가장 비슷한(차이가 최소인) 행렬이 $\hat{A}(k)$이다.
그리고 $A$하고 $\hat{A}(k)$의 차이는 $\sigma_{k+1}$, 즉 $A$의 $k+1$번째 특이값이다.

Rank-$k$ approximation을 하면 원래 행렬과 차이가 생길 수밖에 없다. SVD를 사용하면 그 차이를 최소화할 수 있다!
즉, 가장 좋은 저해상도 이미지 찾기 라고 생각하면 된다.
머신러닝의 image processing, noise filtering, regularization of ill-posed problems(잘못 설정된 문제. 해가 없거나 너무 많거나, 작은 입력 변화에도 해가 엄청 달라지는 경우)에서 사용된다.
Chapter 10의 차원축소와 pca에서도 중요한 역할을 한다.
Ex 4.15 (Finding Structure in Movie Ratings and Consumers (continued))
앞 단원 4.5.3의 Ex 4.14에서 나온 행렬에 low-rank approximation을 적용해볼 것이다.
기존의 영화・사용자 정보 행렬은 아래와 같다.
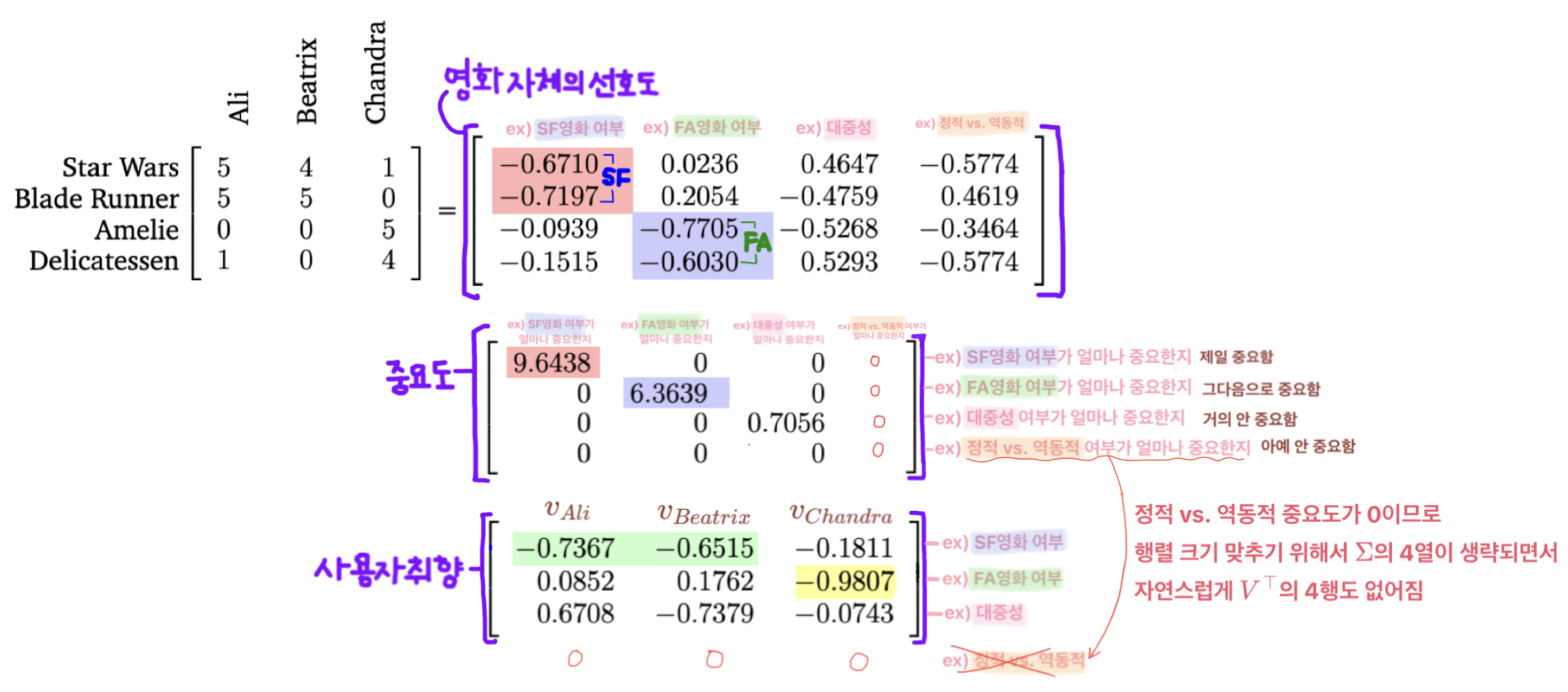
아래는 첫 번째 rank-1 approximation $A_1$를 구성하는 첫 번째 singular value, 그리고 이에 대응하는 left-singular vector, right-singular vector이다.

식으로 표현하면 아래와 같다.
$$\begin{align} A_1 = \sigma_1 u_1 {v_1}^{\top} &= 9.6438 \begin{bmatrix} -0.6710 \\ -0.7197 \\ -0.0939 \\ -0.1515 \end{bmatrix} \begin{bmatrix} -0.7367 & -0.6515 & -0.1811 \end{bmatrix} \\ \\ &= \begin{bmatrix} 4.7672 & 4.2158 & 1.1719 \\ 5.1132 & 2.5218 & 1.2570 \\ 0.6671 & 0.5900 & 0.1640 \\ 1.0763 & 0.9519 & 0.2646 \end{bmatrix} \end{align}$$
두 번째 rank-1 approximation $A_2$도 위랑 비슷하게 해주면 된다.
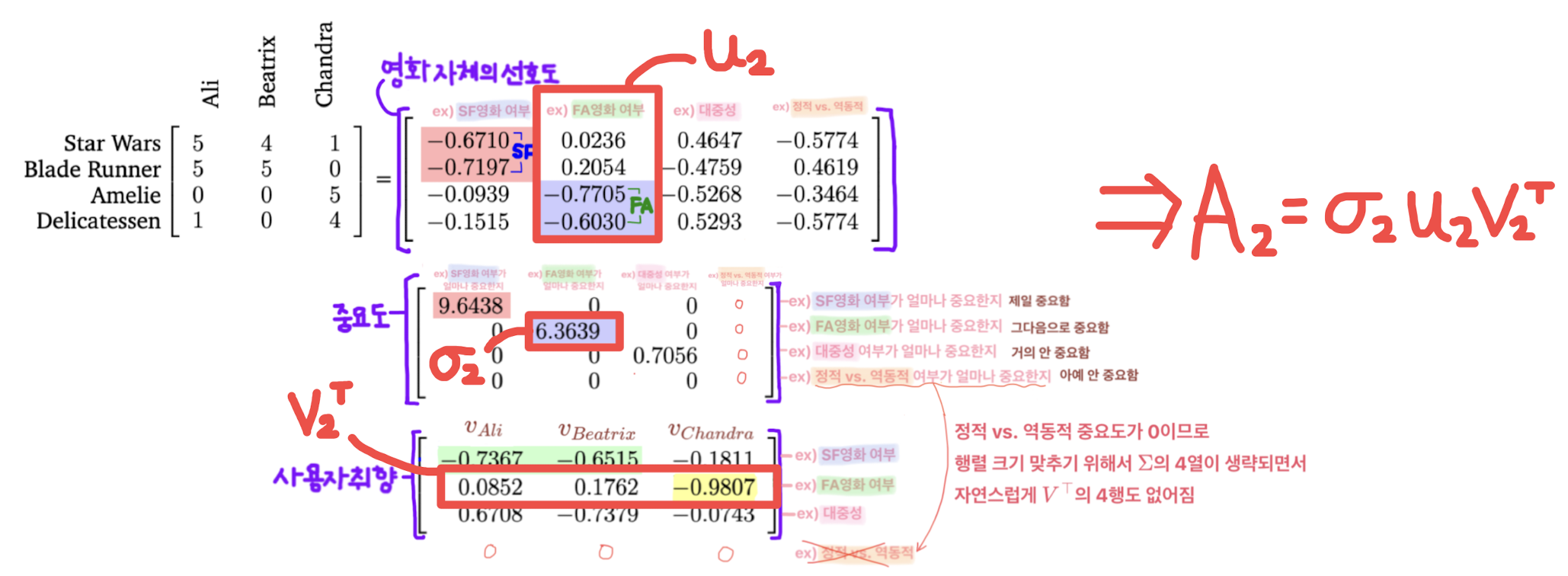
식으로 표현하면 아래와 같다.
$$\begin{align} A_2 = \sigma_2 u_2 {v_2}^{\top} &= 6.3639 \begin{bmatrix} 0.0236 \\ 0.2054 \\ -0.7705 \\ -0.6030 \end{bmatrix} \begin{bmatrix} 0.0852 & 0.1762 & -0.9807 \end{bmatrix} \\ \\ &= \begin{bmatrix} 0.0128 & 0.0265 & -0.1473 \\ 0.1114 & 0.2303 & -1.2819 \\ -0.4178 & -0.8640 & 0.48087 \\ -0.3269 & -0.6762 & 3.7634 \end{bmatrix} \end{align}$$
그래서 최종적으로 $\hat{A}(2) = A_1 + A_2 = \begin{bmatrix} 4.7801 & 4.2419 & 1.0244 \\ 5.2252 & 4.7522 & -0.0250 \\ 0.2493 & -0.2743 & 4.9724 \\ 0.7495 & 0.2756 & 4.0278 \end{bmatrix}$가 된다.
이는 원본 행렬 $A = \begin{bmatrix} 5&4&1 \\ 5&5&0 \\ 0&0&5 \\ 1&0&4 \end{bmatrix}$와 비슷하다!
$A_3$은 영향력이 거의 없기 때문에 무시해도 된다.
따라서 행렬 $A$는 SF영화 여부와 FA영화 여부로 구성된 2차원 행렬임을 알 수 있다!
'선형대수' 카테고리의 다른 글
| [선형대수] Ex 4.1 ~ 4.6 (0) | 2025.03.22 |
|---|---|
| [선형대수] 4.7 Matrix Phylogeny ~ 4.8 Further Reading (0) | 2025.03.20 |
| [선형대수] 4.5.3 Eigenvalue Decomposition vs. Singular Value Decomposition (1) | 2025.03.17 |
| [선형대수] 4.5.2 Construction of the SVD (0) | 2025.03.16 |
| [선형대수] 4.5 Singular Value Decomposition ~ 4.5.1 Geometric Intuitions for the SVD (0) | 2025.03.15 |
