Lecture3: Loss Functions and Optimization
- CS231n 강의 [1]를 듣고 공부한 내용을 나름대로 정리했다.
- 글에 있는 모든 그림과 표는 [2]에서 가져왔다.
~ 목차 ~
1. Loss Function
1.1 Data loss
1.1.1 Multiclass SVM Loss (Hinge Loss)
1.1.2 Cross-entropy Loss (Softmax)
1.1.3 SVM vs. Softmax
1.2 Regularization
2. Optimization
2.1 Random Search
2.2 Follow the slope
2.2.1 Numerical gradient
2.2.2 Analytic gradient
2.2.3 In practice
1. Loss Function
- Loss Function는 손실함수로, classifier가 얼마나 잘 작동하고 있는지 확인하는 역할을 한다.
- 크게 data loss를 구하는 부분이랑 regularization을 주는 부분으로 나눌 수 있다.

1.1 Data loss

- Data loss값인 L을 구하는 단계를 크게 3개로 나눌 수 있다.
① f(xi,W)f(xi,W)값을 구한 다음, 이를 이용해서
② LiLi값을 구하고 이들의
③ 평균을 내면 된다.
- ①의 f(xi,W)f(xi,W)은 Lecture2에서 linear classifier를 사용해서 구했다.
이번 lecture에서도 똑같이 f(xi,W)f(xi,W)값을 구하기 위해 linear classifier를 사용한다.
편의를 위해서 CIFAR-10 중 3개의 클래스만 가져오겠다. 그리고 각 클래스의 f(x,W)값을 아래 표와 같다고 하자.

그 결과,
- 1번째 이미지를 car로 예측했음을 알 수 있다. (오답) (∵f(x,W): cat 3.2, car 5.1, frog -1.7)
- 2번째 이미지를 car로 예측했음을 알 수 있다. (정답) (∵f(x,W): cat 1.3, car 4.9, frog 2.0)
- 3번째 이미지를 car로 예측했음을 알 수 있다. (오답) (∵f(x,W): cat 2.2, car 2.5, frog -3.1)
- ②에서는 '그럼 정답은 얼마나 정답이고, 오답은 얼마나 오답일까?'를 구한다.
즉, LiLi는 classifier가 얼마나 잘 작동하고 있는가'를 나타낸다.
강의에서는 LiLi를 구하는 방법 2가지(Multiclass SVM Loss, Cross-entropy Loss)를 소개한다.
1.1.1 Multiclass SVM Loss (Hinge Loss)

- Multiclass SVM Loss는 위와 같은 공식을 따른다. Hinge loss라고도 한다.
- 다른 라벨의 f(w,X)f(w,X)값에서 정답 라벨의 f(w,X)f(w,X)값을 뺏을 때 차이가 1이상이면 그대로 내보내고,
1미만이면 0으로 절삭한다고 이해하면 된다.
+ check) 식 sj−syi+1sj−syi+1에서의 1은 임계값(그냥 내 느낌..)으로, 사람이 임의로 정하는 값이다.
데이터를 보면서 상황에 맞게 설정해주면 된다.
최종 결과는 어차피 max를 거치기 때문에 임계값에 따라서 크게 영향을 받지는 않는다.
- 이 공식을 바탕으로 1,2,3번째 이미지의 LiLi값들과 최종 LL값을구해보자.

- 즉, 오답이 5.27만큼 오답이라는 것을 알 수 있다.
- 강의에서는 개념을 잘 이해했는지 확인하기 위해 7가지 질문을 던진다.
Q1: What happens to loss if car scores change a bit?
- Car점수가 조금 달라진다고 해서 변화가 생기지는 않는다.
다른 라벨과 정답 라벨의 f(x,W)값 차이가 1보다만 크면 되는데, 이미 차이가 여유롭게 나고 있기 때문이다. (-2.6, -1.9)
Q2: What is the min/max possible loss?
- Min LiLi값은 0이고, max LiLi값은 무한대이다. 공식 생김새를 보면 알 수 있다.
Q3: At initialization W is small so all s≈0s≈0. What is the loss?
- LiLi값은 (클래스 수) -1이 된다.
대부분의 항이 0에 가깝다면 f(x,W)값이 0에 가까워지고, 그럼 (0-0+1)이 ((클래스 수)-1)개만큼 나오게 된다.
초기 단계에서 항상 이 값이 나와야 하기 때문에 디버깅 항으로 사용하기 좋다.
Q4: What if the sum was over all classes? (including j=yij=yi)
- Data loss가 1만큼 증가한다. max(0, (x - x + 1))이 추가되기 때문이다.
Q5: What if we used mean instead of sum?
- Data loss값은 변하겠지만 classifier의 모양은 같다. 그냥 양수로 나눠주는 것이기 때문이다.
Q6: What if we used max(0,sj−syi+1)2max(0,sj−syi+1)2?
- 틀린 항에 대한 패널티가 더 크게 부여된다. 손실함수 값이 제곱이 되기 때문이다.
Q7: Suppose that we found a W such that L=0. Is this W unique?
- 아니다! W에서 L=0이 나왔다면 2W에서도 L=0이 나온다. 아래와 같은 예시에서 확인할 수 있다.
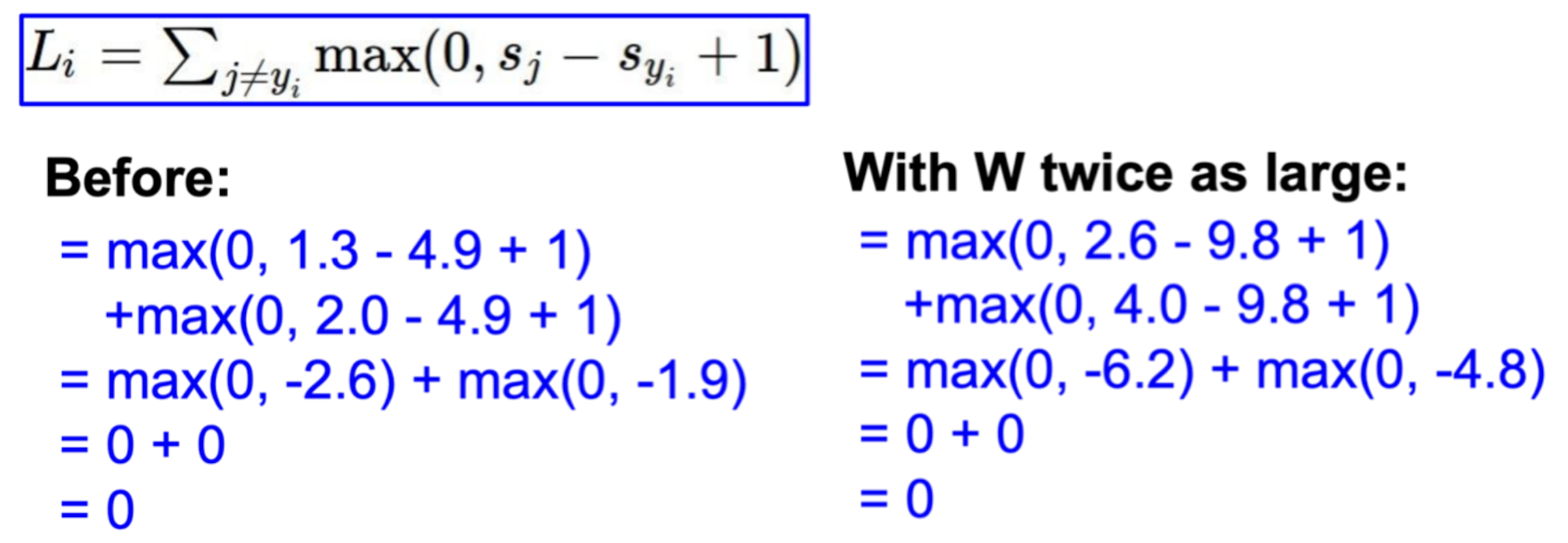
- 이러한 특징을 가진 Multiclass SVM Loss를 다음과 같이 코드로 구현할 수 있다.

- 아쉬운 점이라고 하면, Multiclass SVM Loss에서는 LiLi값 자체에 큰 의미가 없다는 것이다.
그냥 숫자가 상대적으로 크면 오답이 더 오답인 것이고, 숫자가 0에 가까울수록 정답에 가깝다는 것밖에 모른다.
1.1.2 Cross-entropy Loss (Softmax)
- Cross-entropy loss는 흔히 softmax라고 불리는 loss로, 숫자 자체에 의미가 함축되어 있다.
- 기본 공식은 아래와 같다.
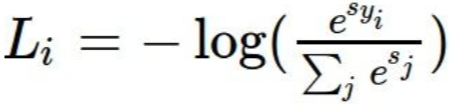
- 아까 나온 cat 사진을 가지고 softmax를 적용해보자. 단계별로 계산해보면 아래와 같다.
지수함수 계산을 한 뒤, 이 값을 가지고 확률을 계산해서 log에 통과시키는 방식이다. 마지막에 부호 맞춰주려고 -를 달아놓는다.

+ Exponential 계산을 하는 이유
→ 손실값 차이를 드라마틱하게 보여주기 위해
- 강의에서는 개념을 잘 이해했는지 확인하기 위해 2가지 질문을 던진다.
Q1: What is the min/max possible loss LiLi?
- Min LiLi값은 0이고, max LiLi값은 무한대이다. x가 0이상 1이하일 때의 -log(x) 그래프를 생각해보면 된다.
Q2: Usually at initialization W is small so all s≈0s≈0. What is the loss?
- log(c)가 된다. 모든 클래스의 SyiSyi에 0을 넣고 계산해보면 된다.
1.1.3 SVM vs. Softmax
- 이제 이 둘을 비교해볼 것이다. 먼저 전체적인 프로세스를 보자면 다음과 같다.
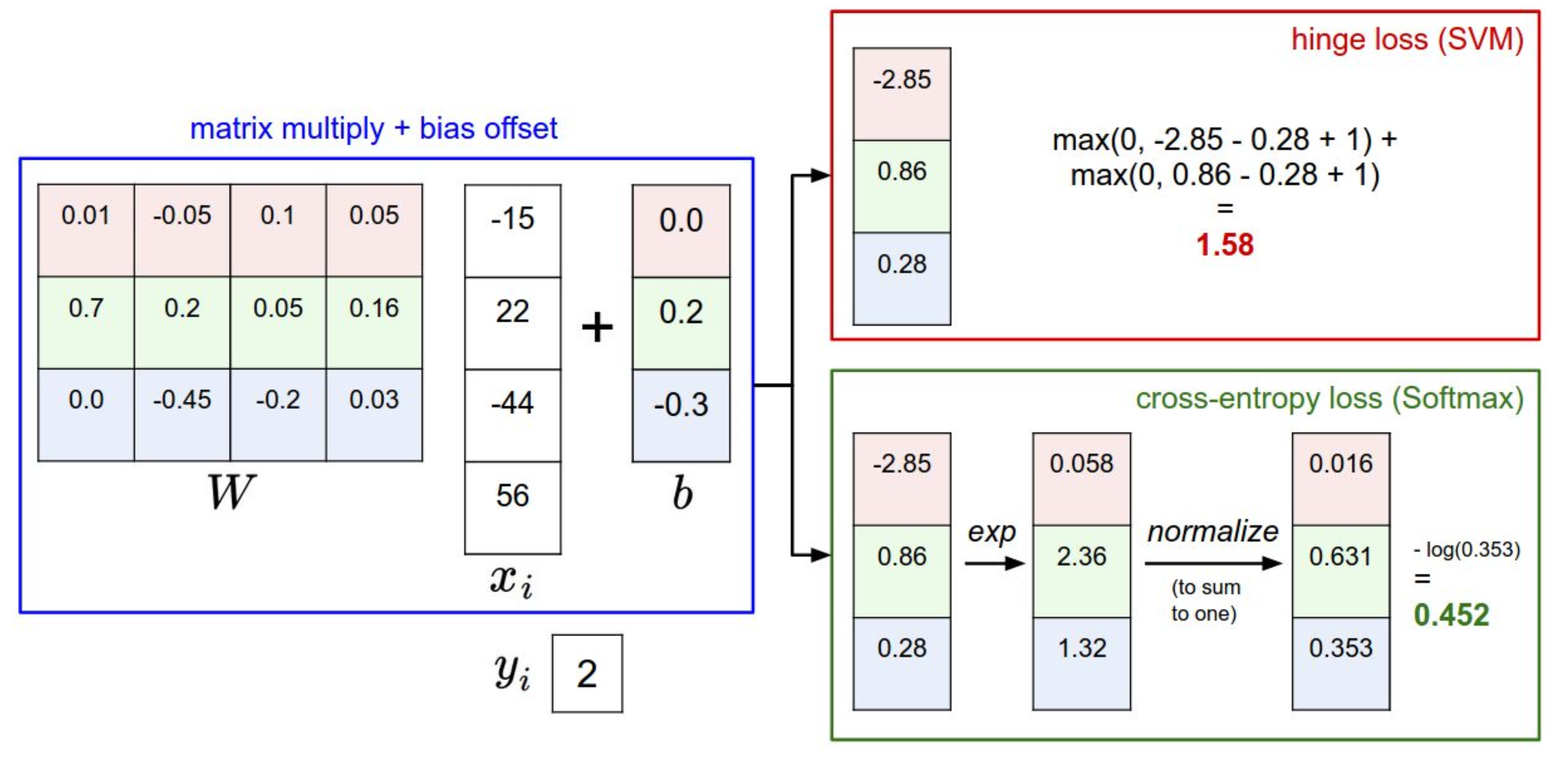
- 그리고 다음은 각각 Softmax와 SVM의 LiLi를 구하는 공식이다.
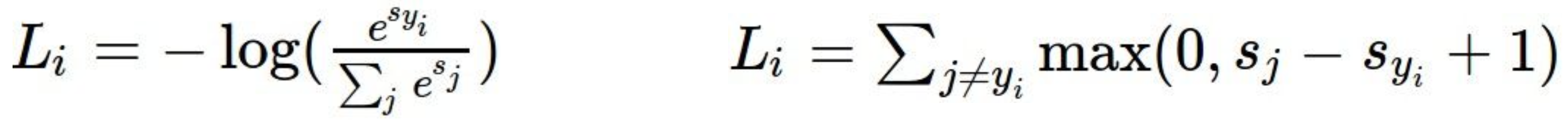
- 비교해보자면 softmax는 최대한 정답 라벨의 손실함수값을 줄이고 오답 라벨의 손실함수값을 늘리려고 하지만,
SVM은 특정 임계값(여기서는 1)을 넘기면 신경을 쓰지 않는다는 것을 알 수 있다.
실제 상황에서 어떤 loss function을 정할지 생각할 때 이러한 특성들을 고려하면서 선택하는 것이 좋다.
1.2 Regularization
- Regularization은 정규화 항으로, 처음에 나왔던 Loss function의 수식에서 2번째항에 해당한다.
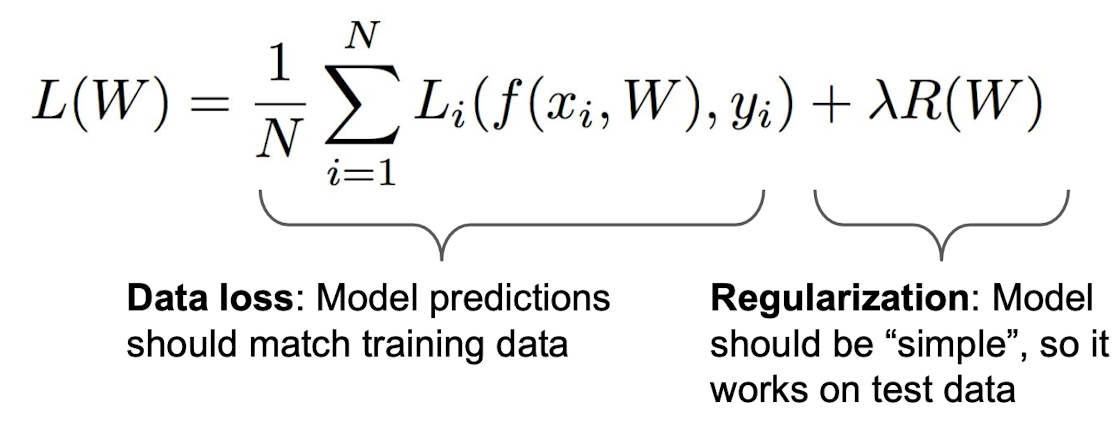
Q: 왜 regularization이 필요할까? Data loss만 구하면 되는거 아닌가?
→ (아래 왼쪽 그래프) Data loss만 구하면 classifier가 오버피팅 될 수 있다.
(아래 중간 그래프) 오버피팅된 classifier는 새로 들어온 데이터를 제대로 분류하지 못한다.
(아래 오른쪽 그래프) Regularization이 적용된 classifier를 사용하면 데이터들을 좀 더 포괄적으로 잘 분류할 수 있다.

- 다양한 종류가 있는데, 여기서는 L2 regularization(weight decay)에 대해서만 구체적으로 설명한다.
- L2 regularization의 식은 다음과 같다. 가중치의 제곱을 계산해서 data loss에 추가하는 형태이다.
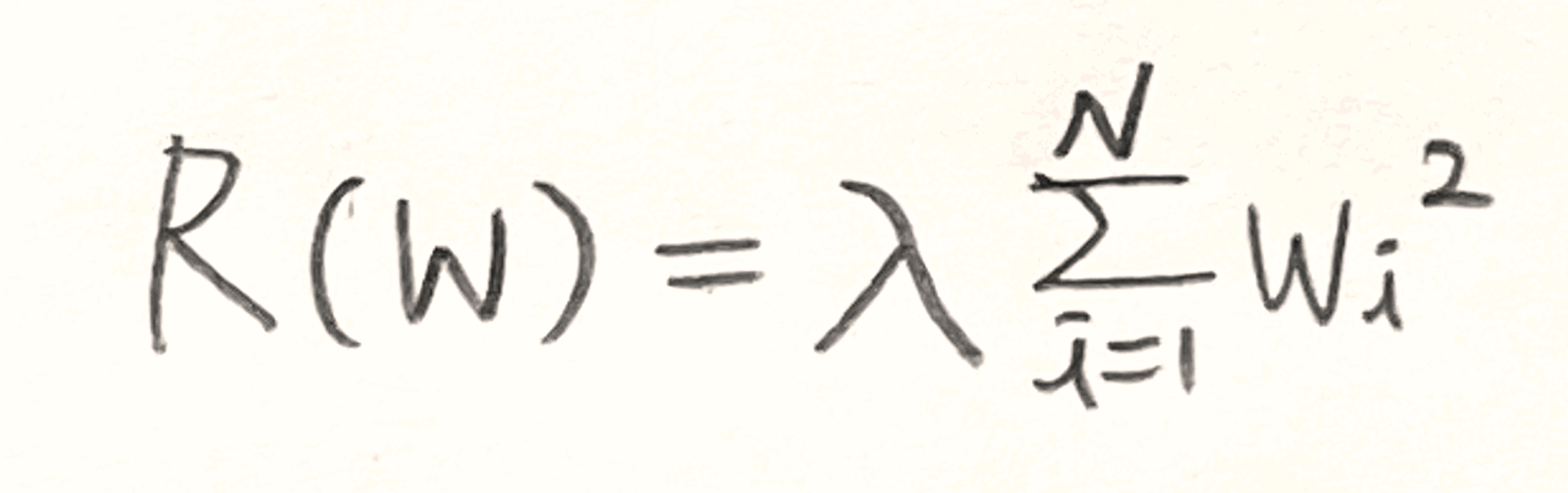
즉, 가중치가 클수록 loss function의 값이 커져서 규제 효과가 나타나게 된다.
가중치에 따른 regularization값은 아래와 같이 계산할 수 있다.
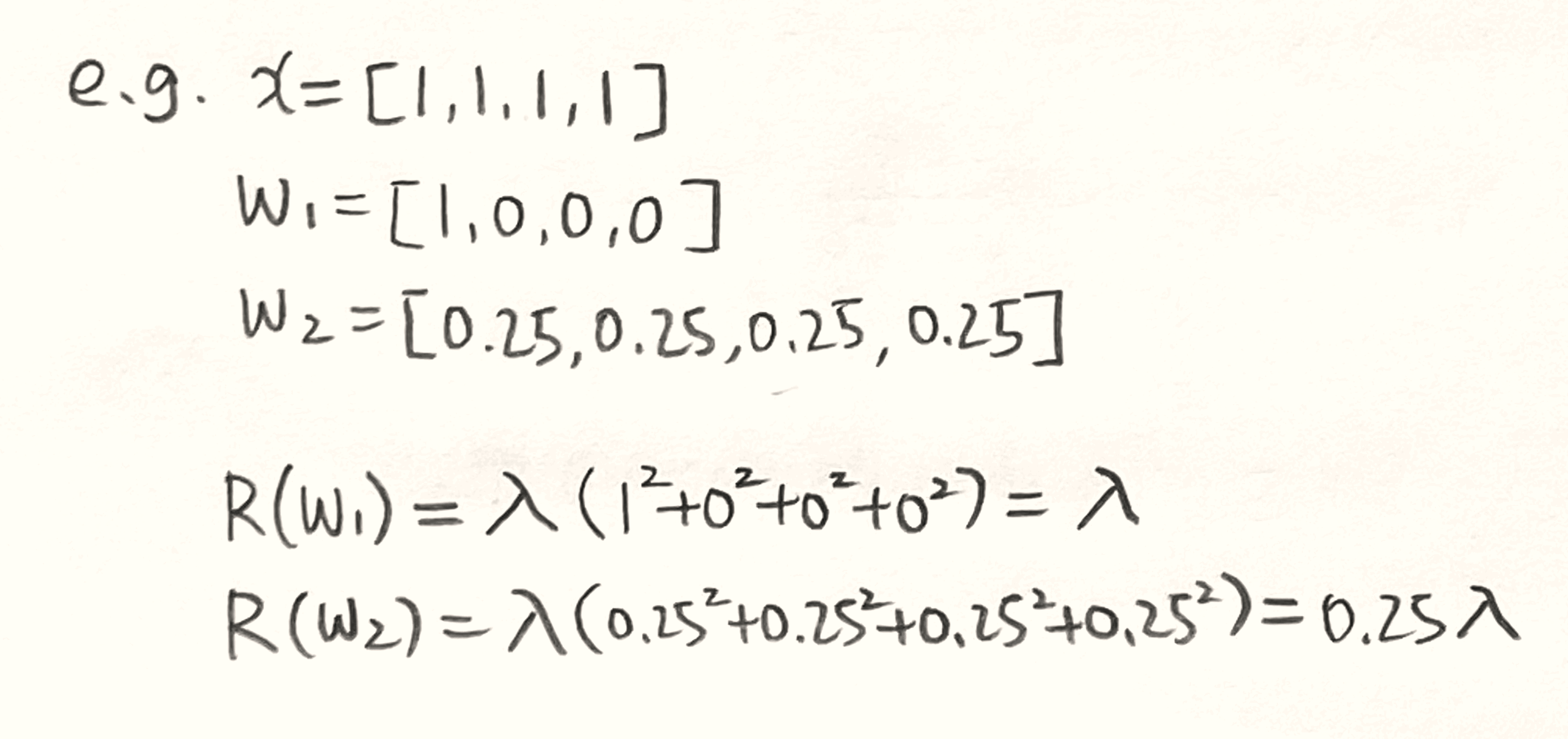
- 여기까지 해서 loss function을 구하는 방법을 알아봤다.
한번 되짚고 넘어가자면, 우리의 목표는 loss function값을 구해서 이를 최소화하는 것이다.
이제 loss function값을 구하는 방법은 알았으니, 이를 최소로 만들기만 하면 된다.
그럼 어떻게 loss function을 최소로 할 수 있을까? 변수는 W이기 때문에, loss function을 최소로 하는 W를 찾으면 된다.
이때 사용되는 방법이 optimization이다.
2. Optimization
- Optimization은 최적화로, 손실을 최소로 하는 W를 찾기 위해 수행된다.
2가지 방법(Random search, Follow the slope)이 소개된다.
2.1 Random Search
- 가장 단순한 방법은 Random Search이다. 말 그대로 W값들을 랜덤하게 넣어보면서 그 중 손실이 최소인 W를 찾는 방법이다.
코드로 구현하면 아래와 같다.
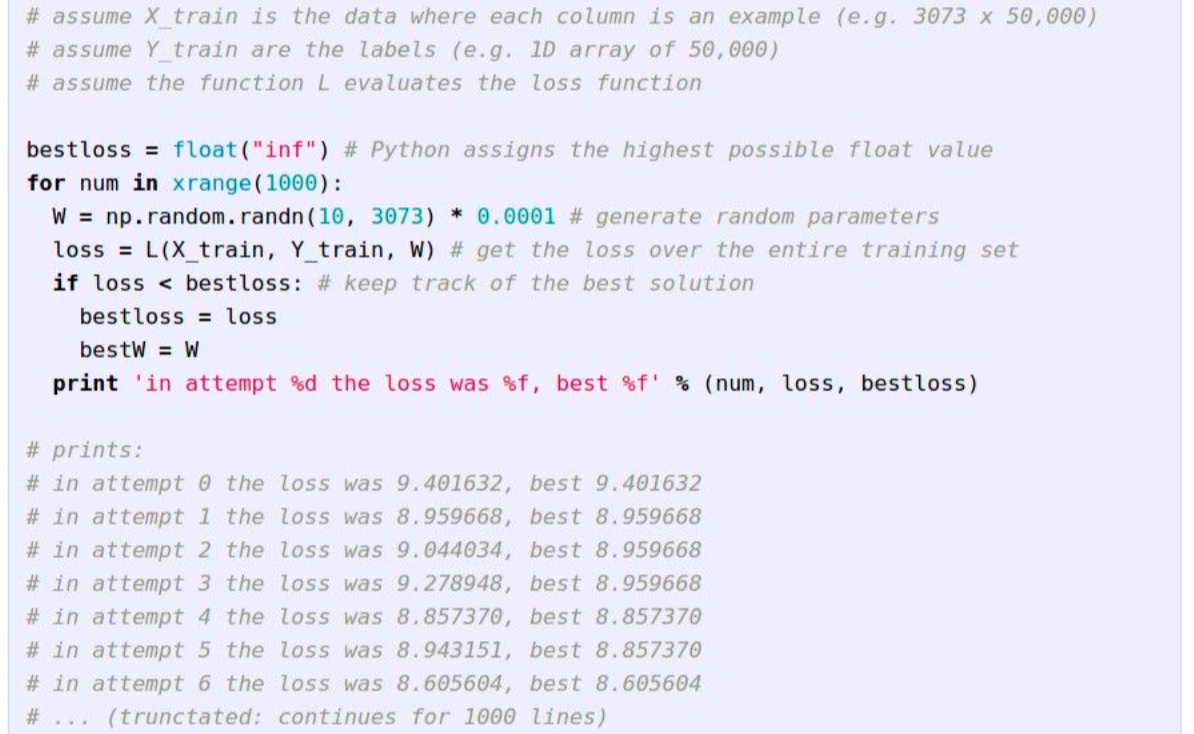
- 강의 왈 'This is a very bad idea..'
- 생각보다 높은 정확도(15.5%)를 내지만 지금 SOTA가 95%임을 감안해보면 한참 보완이 필요한 방법이다.
2.2 Follow the slope
- W값을 찾을 때 기울기를 따라가는 방법이다. 이 방법을 주로 사용한다.
사람이 아래 그림과 같은 굴곡진 곳에 서있다고 생각하고, 자기가 밟고 있는 경사면의 기울기를 느끼면서 이동하는 것이다.

- 기울기를 이용하는 방법에는 2가지(Numerical gradient, Analytic gradient)가 있다.
2.2.1 Numerical gradient
- Numeric gradient는 0에 가까운 h를 활용하여 근사해서 기울기를 구한다.
df(x)dx=limh→0f(x+h)−f(x)hdf(x)dx=limh→0f(x+h)−f(x)h를 사용하는 것이다.
컴퓨터에서는 극한을 구현할 수 없기 때문에 h를 임의의 작은 값 10−510−5로 놓고 계산을 해보겠다.
e.g. f(x)=x2f(x)=x2일 때, df(x)dx=(x+10−5)2−x210−5df(x)dx=(x+10−5)2−x210−5이므로 f(3)≈6f(3)≈6이 된다.
- 이런 식으로 쭉 계산을 하면 아래와 같은 과정을 거쳐야 한다.

- Terrible한 아이디어다. 너무 느리다!
딥러닝 모델에서는 w가 많으면 1억개 이상도 되는데, 기울기를 한번 구하려면 너무 많은 계산을 해야 한다.
- 그래서 하나하나 계산하는 대신에 미분으로 한번에 구해버리는 analytic gradient를 사용한다.
2.2.2 Analytic gradient
- Analytic gradient는 함수를 바로 미분해서 기울기를 구한다.
e.g. f(x)=x2f(x)=x2일 때 df(x)dx=2xdf(x)dx=2x이므로 f(3)=6f(3)=6을 바로 구할 수 있다.
- 이런 식으로 쭉 계산을 하면 아래와 같은 과정을 거친다.

- Numeric gradient보다 계산량이 적고, 근사치가 아닌 정확한 값을 구하고 있음을 알 수 있다.
- 하지만 계산 과정이 error-prone하다는 특징이 있다. 실수하기가 쉽다.
2.2.3 In practice
- Numerical gradient와 analytic gradient의 특징들을 정리하면 다음과 같다.
| Numerical gradient | Analytic gradient |
| 근사치를 구함 | 정확한 값을 구함 |
| 계산속도 느림 | 계산속도 빠름 |
| 사람이 직접 계산하기 쉬움 | 함수에 따라서 사람이 직접 계산하기 어려울 수 있음 |
- 이러한 특징들을 바탕으로 실제 gradient를 구할 때는 analytic gradient를 사용하고,
디버깅 할 때 즉 gradient check를 할 때 numerical gradient를 사용한다.
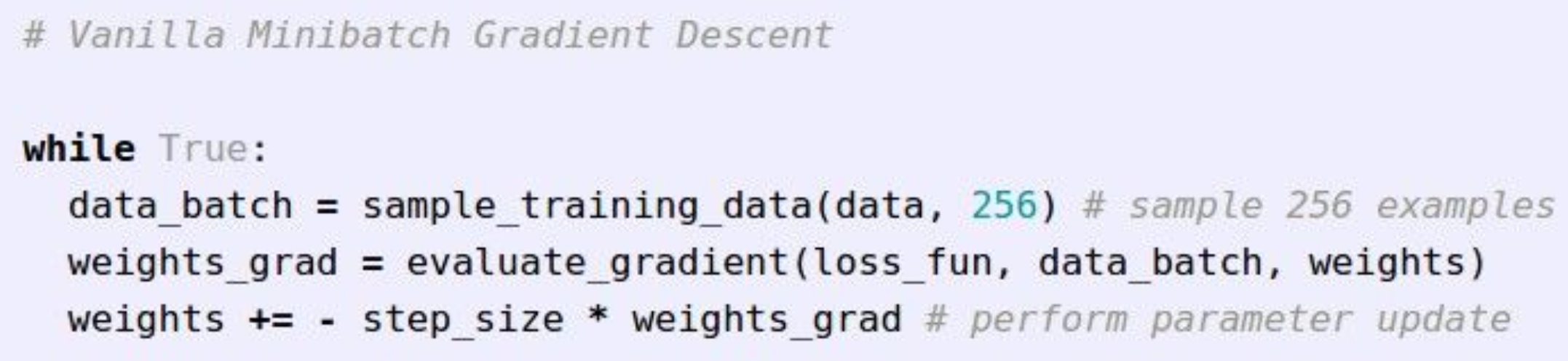
- Gradient를 계산하는 방법으로 gradient descent나 stochastic gradient descent를 구할 수 있다.
코드로 구현하면 다음과 같다.

- 다음 시간에는 back propagation하고 neural networks에 대해서 배울 것이다.
참고문헌
[1] Stanford University, "Lecture3, Loss Functions and Optimization," YouTube, Aug. 12, 2017. [Online]. Available:
https://www.youtube.com/watch?v=h7iBpEHGVNc&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=3
[2] F. Li, J. Johnson, and S. Yeung, "CS231n Convolutional Neural Networks for Visual Recognition: Lecture 3 -Loss Functions and Optimization," Stanford Univ., 2017. [Online]. Available:
https://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture3.pdf
'CS231n' 카테고리의 다른 글
| [CS231n] Lecture7: Training Neural Networks II (1) | 2024.11.22 |
|---|---|
| [CS231n] Lecture6: Training Neural Networks I (0) | 2024.11.21 |
| [CS231n] Lecture5: Convolutional Neural Networks (0) | 2024.11.20 |
| [CS231n] Lecture4: Introduction to Neural Networks (0) | 2024.11.19 |
| [CS231n] Lecture2: Image Classification (2) | 2024.11.17 |