공부하는 단계에서 정리한 내용입니다.
잘못된 내용이 있다면 말씀해주시면 감사하겠습니다.
https://mml-book.github.io/book/mml-book.pdf
3.8 Orthogonal Projections
Projection은 선형변환에서 매우 중요한 개념이다. (e.g. PCA, deep auto-encoder)
머신러닝에서 종종 고차원의 데이터를 다루게 되는데, 고차원 데이터는 분석・시각화하기가 힘들기 때문에 차원을 축소시키는 방법을 사용한다.
고차원 데이터는 몇몇 차원에 정보가 집중되어있기에 가능한 방법이다.
이때, 정보손실을 최소화하기 위해서 가장 중요한 차원을 찾아야 한다. 이를 Orthogonal projection 이라고 한다.
그림으로 나타내면 아래와 같다.

이 방법은 Chapter10의 linear dimensionality reduction과 Chapter12의 classification, 그리고 Chapter9의 linear regression에서 사용된다.
Def 3.10 (Projection)
벡터공간 $V$와 그 부분공간 $U$가 있을 때, 선형변환 $\pi : V \leftarrow U$가 $\pi^{2} = \pi \circ \pi = \pi$을 만족하면 projection이라고 부른다.
즉, $\pi(\pi(v)) = \pi(v)$가 되어야 한다는 뜻이다. 이는 다시 투영해도 결과가 변하지 않음을 의미한다.

2.7에서 공부했듯이 선형변환이 변환행렬로 표현될 수 있기 때문에, projection도 특수한 변환행렬 꼴로 표현될 수 있다.
즉, $(P_{\pi})^{2} = (P_{\pi})$이다.
이제 내적공간 $(\mathbb R_{n}, \langle ・,・ \rangle)$에서 orthogonal projection 하는 방법에 대해서 공부할 것이다.
먼저 1차원 선부터 시작해보자. (+ 책에서 별도로 표기하지 않는 한 내적 계산은 점곱이다!)
3.8.1 Projection onto One-Dimensional Subspaces (Lines)
$\mathbb R^{2}$ 공간에 원점을 지나는 벡터 $b$를 기저벡터로 하는 1차원 부분공간 $U$가 있다고 하자.
여기서 우리는 벡터 $\pi_{U}(x)$($x$를 $U$에 projection 시킨 벡터)를 구해보려고 한다.
먼저 $\pi_{U}(x)$는 다음과 같은 성질을 갖는다. 아래 그림을 보면서 이해해보자.
- $\pi_{U}(x)$는 $x$와 가장 가깝다. 즉, $\| x - \pi_{U}(x) \|$가 최소가 되어야 하므로 $\pi_{U}(x) - x$와 $\pi_{u}(x)$은 수직이다.
따라서 $\langle \pi_{U}(x) - x, b \rangle = 0$이다.
- $\pi_{U}(x)$는 부분공간 $U$에 속한다. 따라서, 임의의 $\lambda$에 대해서 $\pi_{U}(x) = \lambda b$이다.

이제 아래 3 단계를 통해서 $\lambda$, $\pi_{U}(x)$, $P_{\pi}$를 구해볼 것이다.
1. $\lambda$ 구하기
위에서 $\langle \pi_{U}(x) - x, b \rangle = 0$ 이고 $\pi_{U}(x) = \lambda b$ 였으므로 아래와 같이 바꿀 수 있다.
$$\langle \pi_{U}(x) - x, b \rangle = 0 \Longleftrightarrow \langle x- \lambda b, b \rangle = 0$$
그리고 아래와 같은 과정으로부터 $\lambda$를 구할 수 있다.

추가로 여기서 $\| b \| = 1$이면, $\lambda = b^{\top}x$가 된다.
2. $\pi_{U}(x)$ 구하기
위에서 $\pi_{U}(x) = \lambda b$이고 $\lambda = \frac{b^{\top}x}{\| b \|^{2}}$이므로, $\pi_{U}(x) = \lambda b$ = $\frac{b^{\top}x}{\| b \|^{2}}$ $b$ 이다.
그리고 아래와 같은 과정으로부터 $\pi_{U}(x)$를 구할 수 있다.

여기서 $\| x \| = 1$이면, $\pi_{U}(x)$가 $|\cos \omega|$와 같아진다. 아래 그림에서 확인할 수 있다.

3. $P_{\pi}$ 구하기
위에서 $\pi_{U}(x) = \lambda b$이고 $\lambda = \frac{b^{\top}x}{\| b \|^{2}}$이므로, 전개해보면 아래와 같이 나온다.
Projection이 linear mapping이기 때문에 $\pi_{U}(x) = P_{\pi}x$인 $P_{\pi}$가 존재해야 한다.
따라서, 아래와 같이 $P_{\pi} = \frac{b^{\top}b}{\|b\|^2}$이다.

즉, projection matrix $P_{\pi}$가 벡터 $x$를 특정 방향 $b$로 정렬시키는 변환임을 알 수 있다.
Remark.
Projection $\pi_{U}(x)$는 여전히 $n$차원 벡터이다. 하지만 $n$개의 좌표를 알 필요가 없다.
$\pi_{U}(x)$가 기저벡터 b의 배수이므로 $\lambda$ 값만 알면 된다!
Ex 3.10 (Projection onto a Line)
원점을 지나면서 벡터 $b$ 방향으로 뻗어 있는 직선에 $P_{\pi}$를 projection 시켜볼 것이다.
$b = \begin{bmatrix} 1 & 2 & 2 \end{bmatrix}^{\top}$ 라고 하자.
위에서 $P_{\pi} = \frac{b b^{\top}}{b^{\top} b}$임을 알았으므로, 대입해보면 $P_{\pi}$가 아래와 같이 나온다.
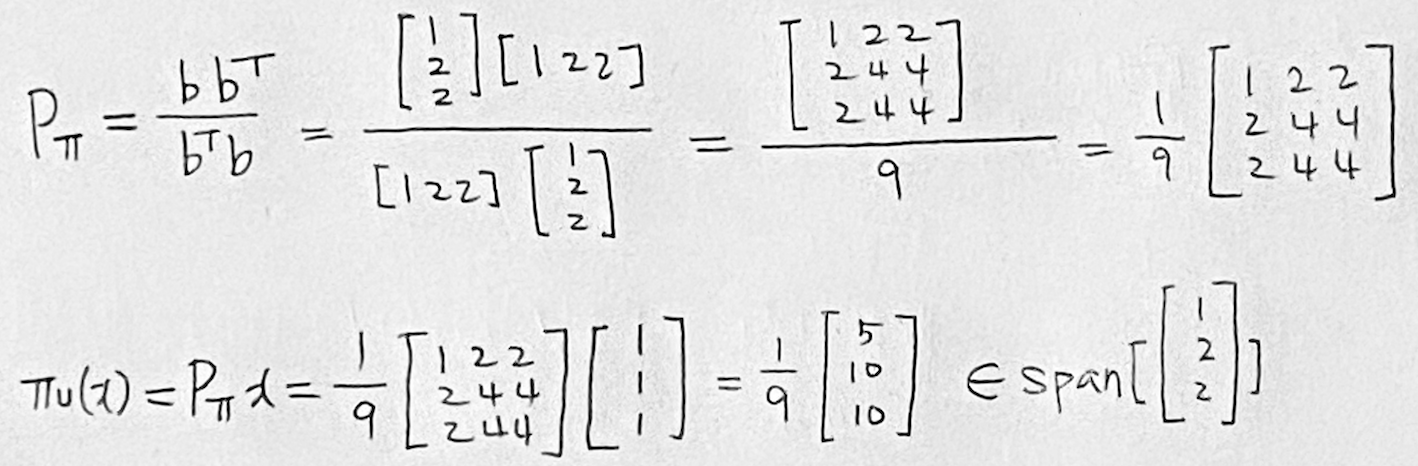
즉, projection의 결과가 벡터 $b$ 위에 있음을 알 수 있다.
(+ projection을 몇 번을 반복해도 결과는 벡터 $b$위에 있다.)
Remark.
Chapter 4에서의 결과를 바탕으로, (아직 안 배움)
$\pi_{U}(x)$가 $P_{\pi}$의 eigenvector이고, eigenvalue는 1임을 알 수 있다.
'선형대수' 카테고리의 다른 글
| [선형대수] 3.8.3 Gram-Schmidt Orthogonalization | 3.8.4 Projection onto Affine Subspaces (0) | 2025.02.21 |
|---|---|
| [선형대수] 3.8.2 Projection onto General Subspaces (0) | 2025.02.19 |
| [선형대수] 3.5 Orthogonal Basis | 3.6 Orthogonal Complement | 3.7 Inner Product of Functions (0) | 2025.02.16 |
| [선형대수] 3.3 Lengths and Distances | 3.4 Angles and Orthogonality (0) | 2025.02.15 |
| [선형대수] 3.2 Inner Products (0) | 2025.02.14 |
