공부하는 단계에서 정리한 내용입니다.
잘못된 내용이 있다면 말씀해주시면 감사하겠습니다.
https://mml-book.github.io/book/mml-book.pdf
3.2 Inner Products
Inner product는 벡터의 길이와 두 벡터 사이의 각도를 직관적으로 알 수 있게 해준다.
주로 벡터들이 서로 orthognal한지 확인하기 위해 사용된다.

3.2.1 Dot Product
Dot Product은 두 벡터를 입력으로 받아서 스칼라 값을 반환하는 연산이다.
$$\mathbf{x}^\top \mathbf{y} = \sum_{i=1}^{n} x_i y_i$$
하지만 inner product는 단순한 dot product보다는 일반적인 개념이다.
3.2.2 General Inner Products
앞에서 우리는 linear mapping(덧셈과 스칼라 곱에 대해서 linear를 유지하는 변환)에 대해서 배웠다.
비슷한 원리로, 이번에는 bilinear mapping 인 $\Omega$ 가 나온다.
$\Omega$는 bilinear라는 말처럼 2개의 입력을 받는 함수이고, 각각의 입력에 대해서 linear하다.
즉, 모든 $x,y,z \in V와 \lambda, \psi \in \mathbb R$에 대해서 아래와 같은 공식을 만족한다.
$$\Omega(\lambda x + \psi y, z) = \lambda \Omega (x,z) + \psi \Omega (y,z)$$
$$\Omega(x, \lambda y + \psi z) = \lambda \Omega (x,y) + \psi \Omega (x,z)$$
식을 보면, $\Omega$가 첫 번째 입력과 두 번째 입력에 대해서 모두 linear하다는 것을 알 수 있다.
Def 3.2 Symmetric, Positive Definite
- 모든 $x,y \in V$에 대해서 $\Omega(x,y) = \Omega(y,x)$이면 $\Omega$가 symmetric하다고 한다.
- 0이 아닌 모든 $x \in V$에 대해서 $\Omega(x,x) > 0$이고 $\Omega(0,0) = 0$이면 $\Omega$를 positive definite라고 한다.

Def 3.3 Inner Product, Inner Product Space
- Symmetric하고 positive definite한 bilinear mapping $\Omega: V x V \to \mathbb R$를 $V$의 inner product라고 한다.
$\Omega(x,y)$ 대신 $\langle x,y \rangle$라고 쓴다.
- 그리고 $(V, \langle \cdot , \cdot \rangle)$를 inner product space 또는 vector space with inner product라고 한다.
$\mathbf{x}^\top \mathbf{y} = \sum_{i=1}^{n} x_i y_i$를 만족하는 dot product를 사용하면 Euclidean vector space라고 한다.

Ex 3.3 (Inner Product That Is Not the Dot Product)
만약 2차원 공간에서 $\langle x, y \rangle := x_{1}y_{1} - (x_{1}y_{2} + x_{2}y_{1}) + 2x_{2}y_{2}$ 일 때,
이건 inner product이긴 하지만 dot product는 아니다. (연습문제에서 증명해보라고 하고 일단 넘어감)
3.2.3 Symmetric, Positive Definite Matrices
$\langle x,y \rangle$는 $\langle \sum_{i=1}^{n} \psi_{i}b_{i}, \sum_{j=1}^{n} \lambda_{j} b_{j} \rangle$로 표현될 수 있고,
여기서 첫 번째 벡터합을 분배하면 $\sum_{i=1}^{n} \psi \langle b_{i}, \sum_{i=1}^{n} \lambda_{j} b_{j} \rangle$ 가 되고,
두 번째 벡터합을 분해하면 $\sum_{i=1}^{n} \sum_{j=1}^{n} \psi \langle b_{i}, b_{j} \rangle \lambda_{j}$가 된다.
이거를 다시 정리하면 $\sum_{i=1}^{n} \psi_{i}(\sum_{j=1}^{n}A_{ij} \lambda_{j})$가 되면서, 결론적으로 $\hat{x}^{\top} A \hat{y}$가 된다고 한다.
(솔직히 와닿지가 않는다. 이렇게 해서 뭘 말하고 싶은거야..? 싶다.
뒤에 있는 연습문제를 풀다보면 이해가 될 것이라고 믿어보며.. 책에 있는 내용만 정리해놓고 일단 넘어가겠다.)
Def 3.4 (Symmetric, Positive Definite Matrix)
벡터공간 $V$에 있는 0이 아닌 모든 $x$에 대해서 $m \times n$ 차원 행렬 $A$가
- $x^{T}Ax >0$이면 symmetric, positive definite 또는 positive definite라고 한다.
- $x^{T}Ax \geqslant 0$이면 symmetric, positive semidefinite라고 한다.

Ex 3.4 (Symmetric, Positive Definite Matrices)
$A_{1} = \begin{bmatrix} 9 & 6 \\ 6 & 5 \end{bmatrix}$이고 $A_{2} = \begin{bmatrix} 9 & 6 \\ 6 & 3 \end{bmatrix}$ 일 때, $A_{1}$은 positive definite 가 맞지만 $A_{2}$는 positive definite가 아니다.
이유는 아래와 같다.

Theorem 3.5
$\langle x,y \rangle = {\hat{x}}^{\top} A \hat{y}$ 이면, $\langle \cdot, \cdot \rangle$이 내적이다!
그리고 이때 $m \times n$행렬 $A$는 symmetric이고 positive definite이어야 한다.
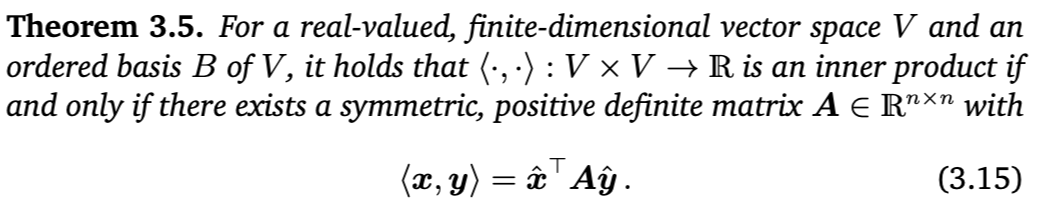
추가적으로, 아래와 같은 성질을 만족한다.
- 행렬 $A$의 null space은 0벡터만 포함한다. 즉, $x \neq 0$이면 $Ax \neq 0$이다. ($\because x \neq 0$일 때 $x^{\top} A x > 0$)
- 행렬 $A$의 diagonal element들은 항상 양수이다. ($\because a_{ii} = e_{i}^{top} A e_{i} > 0$)
'선형대수' 카테고리의 다른 글
| [선형대수] 3.5 Orthogonal Basis | 3.6 Orthogonal Complement | 3.7 Inner Product of Functions (0) | 2025.02.16 |
|---|---|
| [선형대수] 3.3 Lengths and Distances | 3.4 Angles and Orthogonality (0) | 2025.02.15 |
| [선형대수] 3 Analytic Geometry | 3.1 Norms (0) | 2025.02.13 |
| [선형대수] Exercise 2.11 - 2.20 (0) | 2025.02.09 |
| [선형대수] Exercises 2.1 ~ 2.10 (0) | 2025.02.02 |
