기본기 쌓기의 일환으로 'Attention is all you need' 논문, 일명 transformer 논문을 리뷰해보려고 한다.
https://papers.nips.cc/paper_files/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf
내가 가장 처음으로 읽은 AI 논문이다. 1회독 할 때는 약 일주일동안 머리싸매고 읽어가면서 겨우 감만 잡았던 기억이 있다.
읽고 나서 너무 뿌듯했지만 정리할만큼의 이해를 하지는 못했던 것 같다.
이번이 약 3회독짼데, 그동안 개념이 숙성되었기를 바라면서 한번 정리를 시작해보겠다.
주요 부분인 Section 3,4,7 (모델 구조, 모델 사용이유, 결론)만 정리해보았다.
3. Model Architecture
성능 좋은 *시퀀스 변환 모델들은 보통 인코더-디코더 구조를 가지고 있음
*시퀀스 변환 모델: 한 시퀀스를 다른 시퀀스로 바꾸는 모델
e.g. 영어 -> 한국어, 긴 문장 -> 요약 문장
여기서 인코더는 입력 시퀀스 $(x_1, \cdots, x_n)$를 연속적인 표현벡터 $z=(z_1, \cdots, z_n)$로 변환함
예를 들어서 'I love deep learning'이라는 문장이 있다면 얘를 아래와 같이 토큰화 함
$x_1$ = 'I', $x_2$ = 'love', $x_3$ = 'deep', $x_4$ = 'learning'
그러고 각 토큰들을 아래처럼 임베딩 벡터로 바꿈
"I" -> [0.12, -0.83, 1.04, ...], "love" -> [-0.45, 0.91, 0.33, ...],
"deep" -> [1.20, -0.22, 0.58, ...], "learning"-> [-0.77, 0.44, 1.10, ...]
이게 이산적인 symbol을 연속적인 실수 벡터로 바꾼 거임
여기에 positional encoding을 더하고, 이걸 self-attention하고 FFN에 통과시켜주면 됨
그러면 z들이 나옴
여기까지가 인코더에서 벌어지는 일이고
디코더에서는 이전에 생성한 $y$들 + 인코더 출 $z$ 로부터 출력 $(y_1, \cdots, y_m)$을 차례대로 생성함
Transformer도 큰 틀은 똑같지만 **stacked self-attention을 사용함
**stacked: 여러 층으로 겹겹이 쌓여있다는 뜻
기존 모델과 transformer를 비교해보자면
- 기존 모델들: 인코더 RNN 디코더 RNN+attention
- Transformer: 인코더랑 디코더 둘 다 self-attention + ***point-wise FFN (+디코더에는 masked self-attention)
***point-wise: 각 point들을 따로 처리한다는 뜻
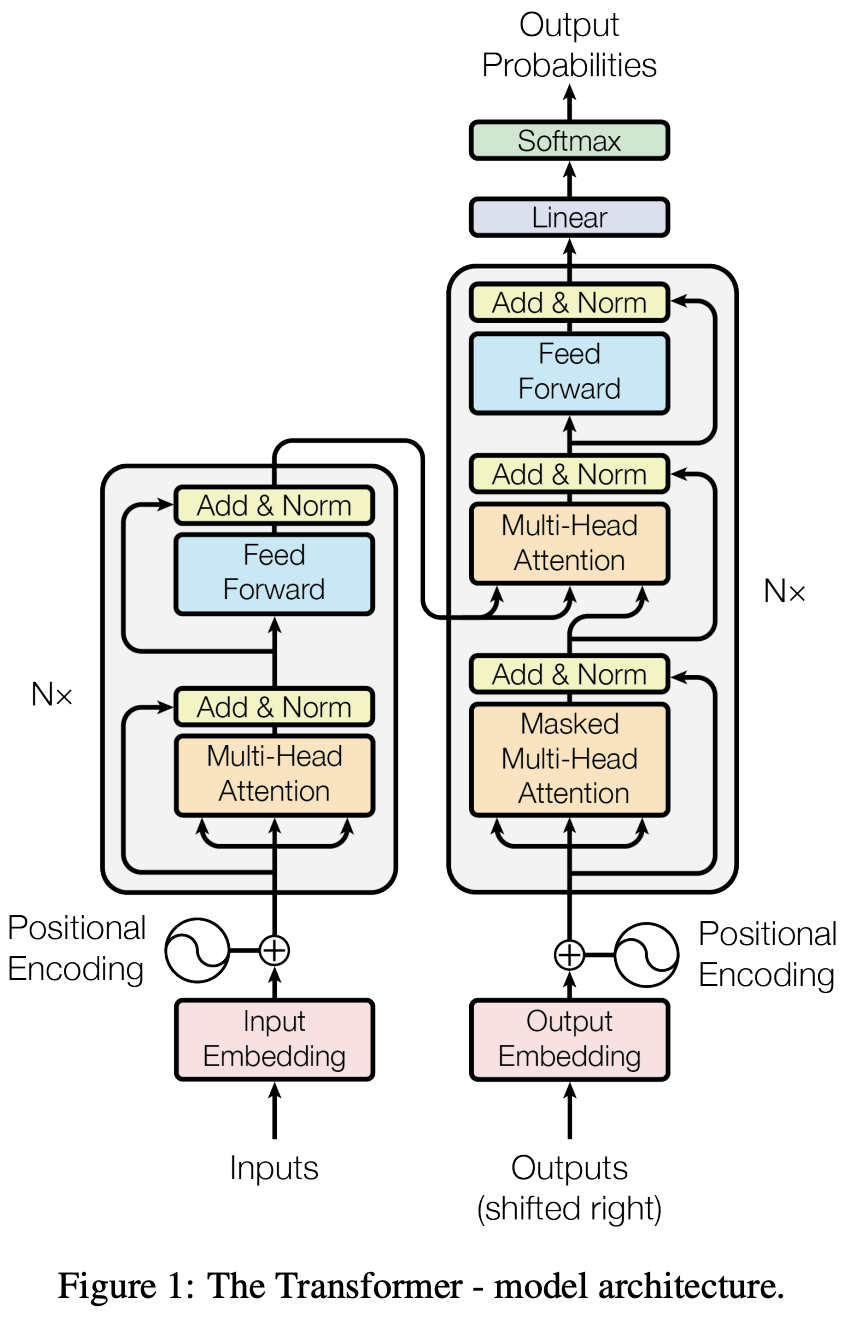
3.1 Encoder and Decoder Stacks
Encoder
같은 레이어 6개로 구성됨. 그리고 각각의 레이어에 2개의 sub레이어가 있음
- sub레이어1: multi-head self-attention 메커니즘
- sub레이어2: 간단한 positionwise FFN
각 sub레이어의 출력은 $LayerNorm(x+Sublayer(x))$ 임
(x: 해당 sub레이어로 들어가는 입력벡터)
여기서 알 수 있는 것
1. $x+Sublayer(x)$: residual 꼴임
Residual 적용하기 위해서는 x랑 Sublayer(x)의 차원이 같아야 하므로
모든 sub레이어와 임베딩레이어의 출력을 $d$=512로 맞춤
2. $LayerNorm$: 그 다음에 layer normalization 적용함
Decoder
디코더도 같은 레이어 6개로 구성됨. 그리고 각각의 레이어에 3개의 sub레이어가 있음
- sub레이어1: *masked self-attention (self-attention은 인코더와 동일하지만 masked가 추가됨)
=> *masked + **shifted 성질로 인해서 위치 $i$에서의 예측은 $i$보다 앞에 있는 출력들만 볼 수 있음
표로 나타내면 아래와 같음
| 예측 위치 | decoder가 볼 수 있는 것 | 예측 대상 |
| 1 | <BOS> | y₁ |
| 2 | <BOS>, y₁ | y₂ |
| 3 | <BOS>, y₁, y₂ | y₃ |
| 4 | <BOS>, y₁, y₂, y₃ | y₄ |
*masked: 마스킹 해놨다는 뜻 (∵ 자기보다 뒤를 못보게 하기 위해)
**shifted: 앞에 <BOS> 토큰을 넣어서 전체를 한칸 shift 시킴 (∵ $i$에서 $y_i$를 못보도록 하기 위해)
- sub레이어2: 인코더 출력에 대한 multi-head attention (추가됨★)
- sub레이어3: positionwise FFN (인코더와 동일)
디코더도 똑같이 $LayerNorm(x+Sublayer(x))$ 형태다.
3.2 Attention
Attention 함수는 $q$,$k$,$v$를 입력받아서 하나의 출력으로 매핑하는 함수라고 할 수 있음 (얘네들은 모두 벡터임)
출력값은 $q$,$k$ 유사도 구해서 가중치 변환시켜서 그 가중치를 바탕으로 $v$를 가중합시켜서 구함
3.2.1 Scaled Dot-Product Attention
여기서는 여러 가지 어텐션 종류 중 scaled dot-product이라는 어텐션을 사용함
(아니 어텐션이 여러 종류가 있다고? 다음에 글 파서 정리해봐야지)
그냥 일반적으로 additive attention하고 dot-product attention이 가장 많이 사용됨
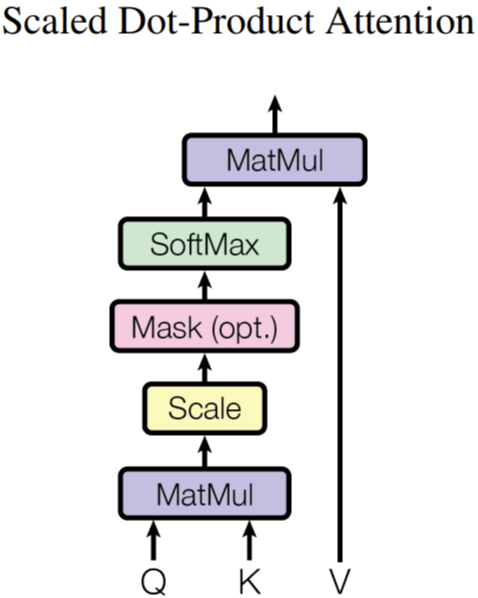
Additive attention은 $q$랑 $k$를 각각 선형변환시켜서 둘을 더한 다음에 $tanh$ 통과시키고 선형변환 시켜서 점수를 생성함
수식으로 표현하자면 아래와 같음
$score(q,k)=v^{\top}tanh(W_q q + W_k k)$
비선형 관계까지 학습 가능함
아 정리하다보니 삼천포로 빠졌는데 다시 돌아와보자면
어쨋든 기본 계산은 dot-product attention이 훨씬 빠르고 효율적인데 $d_k$가 커질수록 분산이 비례해서 커져서 softmax거치면 기울기가 0에 수렴되면서 additive attention보다 성능이 떨어져서
$\sqrt{d_k}$를 나눠서 정규화를 시킨 scaled dot-product attention을 사용함
(+ 별건 아니지만 하필이면 왜 다른 숫자도 아니고 굳이 $\sqrt{d_k}$로 나누는가?에 대해서 정리를 해봣습니다.)

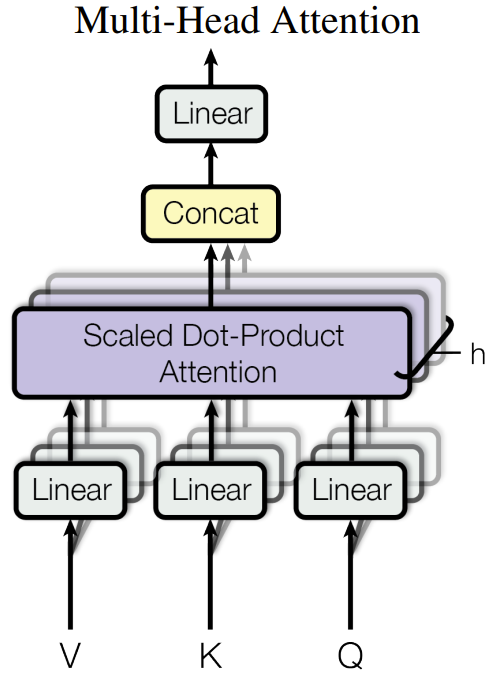
3.2.2. Multi-Head Attention
$d_{model}$ 차원의 $q$, $k$, $v$를 한번만 쓰지 말고
서로 다른 선형변환을 이용해서 각각 다른 차원($d_q$, $d_k$, $d_v$)으로 $h$번 투영하는 것이 효과적임을 발견함
즉, 뭔가 하나의 큰 시선으로 보는 것보다 여러 개의 이런저런 시선으로 봤을 때 더 좋다는 거
논문에서는 $h=8$로 했음
그래서 $d_k$ = $d_v$ = $\frac{d_{model}}{h}$ = 64
3.2.3 Application of Attention in our Model
Transformer에서는 multi-head attention을 3가지 방식으로 사용함
· Encoder-decoder attention 레이어
Seq2seq 모델에서 사용되던 encoder-decoder attention 메커니즘을 모방함
디코더의 모든 위치가 입력 시퀀스의 모든 위치를 참조할 수 있게 됨
· Encoder Self-Attention
· Decoder Self-Attention
(보완 필요)
3.3 Position-wise Feed-Foward Networks
Attention 뒤에 FFN이 들어가게 되는데, 이 FFN은 선형변환+ReLU+선형변환 으로 이루어져있음. 식으로 표현하면 아래와 같음
$FFN(x)= max(0,x W_1+b_1)W_2+b_2$
커널 크기가 1인 두개의 convolution으로도 볼 수 있음 (오!)
같은 레이어 안에서는 모든 position에 대해서 $W$랑 $b$가 같지만 다른 레이어에서는 다름
차원은 $d_{입력}=512$, $d_{은닉층}=2048$, $d_{출력}=512$ 임
(+ 여기서 position-wise하다는 건 각각의 $x_1, \cdots, x_k$가 각각각 처리된다는 뜻임)
3.4 Embeddings and Softmax
다른 시퀀스 변환 모델들처럼 인코더 입력과 디코더 입 토근을 각각 d_{model} 차원으로 변환함
그리고 디코더 출력을 선형변환하고 softmax에 통과시켜서 확률분포로 변환함
그리고! 여기서 신기한 점
임베딩 레이어 2개(인코더 맨 앞, 디코더 맨 앞)랑 pre-softmax linear transformation(디코더 맨 끝)이 모두 같은 가중치를 씀!
임베딩 레이어에서는 가중치에 $\sqrt{d_{model}}$을 곱해서 사용함
(+ 별건 아니지만 하필이면 왜 다른 숫자도 아니고 굳이 $\sqrt{d_k}$를 곱하는가?에 대해서 정리를 해봤습니다.)
3.5 Positional Encoding
4. Why Self-Attention
RNN, CNN 이 아니라 왜 하필이면 Self-Attention을 선택했는가
① 한 layer 당 전체 계산복잡도
- RNN: $O(nd^2)$
- CNN: $O(knd^2)$
( ∵ 커널이 $k$개의 단어를 동시에 처리해야 하므로 RNN의 $k$배)
- Self-Attention: $O(n^2d)$ ($n$: 입력길이, $d$:차원)
② 병렬화 가능한 계산량
- RNN: 병렬화 불가능
- CNN: 병렬화 일부 가능 (동시에 처리 가능한만큼만)
- Self-Attention: 병렬화 가능
③ 장기의존성을 연결하는 연산 단계 수
- RNN: 순차적 처리이므로 긴 경로 필요 -> gradient vanishing 문제
- CNN: 커널이 국소적이므로 여러 계층을 거쳐야 먼 단어에 도달 가능
- Self-Attention: 모든 단어가 모든 단어와 직접 연결 -> path length = 1
Attention은 “어떤 단어가 어느 단어에 집중했는가”를 확률 분포 형태로 시각화 가능.
7. Conclusion
이렇게 최초로 RNN없이 attention에만 기반을 두는 Transformer 모델을 제안했다. 기존 인코더-디코더 구조에서 흔히 사용되던 recurrent layer들을 multi-headed self-attention 으로 대체했다. -> 시간의 순차적 처리 없이도 문맥정보를 학습할 수 있음
번역과제에서는 Transformer 가 RNN 혹은 CNN보다 훨씬 빠르다. (∵ RNN, CNN은 순차처리, Transformer는 병렬처리)
WMT라는 대회에서 증명됨. Transformer가 기존의 모든 앙상블 모델보다도 빠름
이후 과제
번역과제뿐만 아니라 다른 분야에서도 적용할거임 (실제로 번역뿐만 아니라 BERT, GPT. ViT와 같이 확대적용됨)
생성과장을 less sequential 하게 만드는 것을 시도해볼 예정임